题目内容

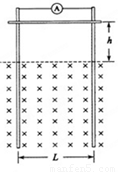
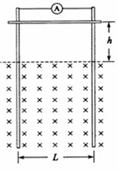
如图，两足够长的光滑平行金属导轨竖直放置，相距为L，一理想电流表与两导轨相连，匀强磁场与导轨平面垂直，一质量为m的导体棒在距离磁场上边界h处由静止释放，导体棒进入磁场后，流经电流表的电流逐渐减小，最终稳定为I。整个运动过程中导体棒与导轨接触良好，且始终保持水平，导体棒在此电路中的有效电阻为R，不计导轨的电阻。求：

（1）磁感应强度的大小B；

（2）电流稳定后，导体棒运动速度的大小v；

（3）流经电流表电流的最大值Im。

 


解析：（1）电流稳定后，导体棒做匀速运动

              由 BIL = mg     ( 2分)             得 B = mg/IL   ( 1分)

（2）由感应电动势E=BLv  ( 1分)    又有I=E/R   ( 1分)

     故可得 v=I2R/mg    ( 1分)

  ( 3) 由题意可知，导体棒刚进入磁场时速度最大，设为Vm ，

    根据机械能守恒1/2 mVm2 = mgh  ( 1分)  感应电动势的最大值 Em = BLVm  ( 1分)

感应电流的最大值 Im = Em /R    ( 1分)   联立解得   ( 1分)

练习册系列答案
相关题目
如图，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨放在水平面上，导轨电阻不计．磁感应强度为B的匀强磁场垂直导轨平面向上，金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨电接触良好，金属棒的质量为m、电阻为R．灯泡的电阻RL=3R，调节电阻箱电阻R1=6R，现给金属棒施加水平向右的恒力F，使棒由静止开始运动，试求：
（1）金属棒运动的最大速度为多大？
（2）当金属棒运动距离为S0时速度恰达到最大，求金属棒由静止开始运动2S0的过程中，整个电路上产生的电热能？
（3）R1为何值时，R1上消耗的电功率最大？最大电功率为多少？

（09年汉沽一中月考）（16分）如图所示,足够长的光滑平行导轨MN、PQ倾斜放置, 两导轨间的距离为L=1.0m,导轨平面与水平面间的夹角为300,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值为R=3.5Ω的电阻,金属棒ab垂直于导轨放置, 金属棒ab的质量m=0.20kg, 电阻r=0.50Ω , 并与导轨保持良好接触. 现在ab上作用一恒力F=5.0N , 方向垂直于ab并沿导轨平面向上,使金属棒ab由静止开始运动,在M处安装一个距离传感器(图中未画出), 可以测出金属棒ab在运动中离MP的距离与时间的该关系,如下表所示.不计导轨的电阻,取g=10m/s2 .求:

 

时间t/s

0

0.10

0.20

0.30

0.40

0.50

0.60

棒离MP的距离s/m

0.01

0.06

0.18

0.36

0.61

1.01

1.41

 

（1）所加磁场的磁感应强度B为多大?

（2）电阻R在0.6s内产生的热量为多少?

（10分）如图，两足够长的光滑平行金属导轨竖直放置，相距为L，一理想电流表与两导轨相连，匀强磁场与导轨平面垂直，一质量为m的导体棒在距离磁场上边界h处由静止释放，导体棒进入磁场后，流经电流表的电流逐渐减小，最终稳定为I。整个运动过程中导体棒与导轨接触良好，且始终保持水平，导体棒在此电路中的有效电阻为R，不计导轨的电阻。求：

（1）磁感应强度的大小B；

（2）电流稳定后，导体棒运动速度的大小v；

（3）流经电流表电流的最大值Im。

 

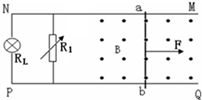（14分）如图，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨放在水平面上，    导轨电阻不计．磁感应强度为B的匀强磁场垂直导轨平面向上，长为￡的金属棒ab垂    直于MN、PQ放置在导轨上，且始终与导轨电接触良好，金属棒的质量为m、电阻为R．两    金属导轨的N、O端连接右端电路，灯泡的电阻RL=4R，定值电阻RL=2R，电阻箱电阻调到使R2=12R，重力加速度为g，现给金属棒水平向左的垂直棒ab方向的恒力F作用，    使棒由静止开始运动，试求：

   （1）金属棒运动的最大速度为多大?

   （2）当金属棒运动距离为S0时速度恰达到最大，求金属棒由静止开始运动2S0的过程中，  整个电路产生的电热；

   （3）R2为何值时，其消耗的功率最大?消耗的最大功率为多少?
 
 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网