题目内容
(2010?安徽)如图1所示,宽度为d的竖直狭长区域内(边界为L1、L2),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为E0,E>0表示电场方向竖直向上.t=0时,一带正电、质量为m的微粒从左边界上的N1点以水平速度v射入该区域,沿直线运动到Q点后,做一次完整的圆周运动,再沿直线运动到右边界上的N2点.Q为线段N1N2的中点,重力加速度为g.上述d、E0、m、v、g为已知量.

(1)求微粒所带电荷量q和磁感应强度B的大小;
(2)求电场变化的周期T;
(3)改变宽度d,使微粒仍能按上述运动过程通过相应宽度的区域,求T的最小值.

(1)求微粒所带电荷量q和磁感应强度B的大小;
(2)求电场变化的周期T;
(3)改变宽度d,使微粒仍能按上述运动过程通过相应宽度的区域,求T的最小值.
分析:根据物体的运动性质结合物理情景确定物体的受力情况.再根据受力分析列出相应等式解决问题.
解答:解:(1)根据题意,微粒做圆周运动,洛伦兹力完全提供向心力,重力与电场力平衡,
则mg=qE0-------①
∵微粒水平向右做直线运动,∴竖直方向合力为0.
则 mg+qE0=qvB-----②
联立①②得:q=
------③B=
--------④
(2)设微粒从N1运动到Q的时间为t1,作圆周运动的周期为t2,
则
=vt1-----⑤qvB=m
--------⑥2πR=vt2------------⑦
联立③④⑤⑥⑦得:t1=
,t2=
--------⑧
电场变化的周期T=t1+t2=
+
-------⑨
(3)若微粒能完成题述的运动过程,要求 d≥2R------⑩
联立③④⑥得:R=
,设N1Q段直线运动的最短时间t1min,由⑤⑩得t1min=
,
因t2不变,T的最小值 Tmin=t1min+t2=
.
答:(1)微粒所带电荷量q为
,磁感应强度B的大小为
.
(2)电场变化的周期T为
+
.
(3)T的最小值为
.
则mg=qE0-------①
∵微粒水平向右做直线运动,∴竖直方向合力为0.
则 mg+qE0=qvB-----②
联立①②得:q=
| mg |
| E0 |
| 2E0 |
| v |
(2)设微粒从N1运动到Q的时间为t1,作圆周运动的周期为t2,
则
| d |
| 2 |
| v2 |
| R |
联立③④⑤⑥⑦得:t1=
| d |
| 2v |
| πv |
| g |
电场变化的周期T=t1+t2=
| d |
| 2v |
| πv |
| g |
(3)若微粒能完成题述的运动过程,要求 d≥2R------⑩
联立③④⑥得:R=
| v2 |
| 2g |
| v |
| 2g |
因t2不变,T的最小值 Tmin=t1min+t2=
| (2π+1)v |
| 2g |
答:(1)微粒所带电荷量q为
| mg |
| E0 |
| 2E0 |
| v |
(2)电场变化的周期T为
| d |
| 2v |
| πv |
| g |
(3)T的最小值为
| (2π+1)v |
| 2g |
点评:运动与力是紧密联系的,通过运动情况研究物体受力情况是解决问题的一个重要思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010?安徽)质量为2kg的物体在水平推力F的作用下沿水平面作直线运动,一段时间后撤去F,其运动的v-t图象如图.g取10m/s2,求:
(2010?安徽)质量为2kg的物体在水平推力F的作用下沿水平面作直线运动,一段时间后撤去F,其运动的v-t图象如图.g取10m/s2,求: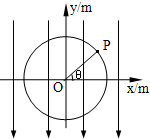 (2010?安徽)如图所示,在xOy平面内有一个以O为圆心、半径R=0.1m的圆,P为圆周上的一点,O、P两点连线与x轴正方向的夹角为θ.若空间存在沿y轴负方向的匀强电场,场强大小E=
(2010?安徽)如图所示,在xOy平面内有一个以O为圆心、半径R=0.1m的圆,P为圆周上的一点,O、P两点连线与x轴正方向的夹角为θ.若空间存在沿y轴负方向的匀强电场,场强大小E=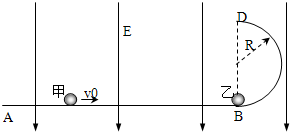 (2010?安徽)如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103 V/m.一不带电的绝缘小球甲,以速度v0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞.已知甲、乙两球的质量均为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,g取10m/s2.(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)
(2010?安徽)如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103 V/m.一不带电的绝缘小球甲,以速度v0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞.已知甲、乙两球的质量均为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,g取10m/s2.(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)  (2010?安徽)如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个边长相等的单匝闭合正方形线圈Ⅰ和Ⅱ,分别用相同材料,不同粗细的导线绕制(Ⅰ为细导线).两线圈在距磁场上界面h高处由静止开始自由下落,再进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈Ⅰ、Ⅱ落地时的速度大小分别为v1、v2,在磁场中运动时产生的热量分别为Q1、Q2.不计空气阻力,则( )
(2010?安徽)如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个边长相等的单匝闭合正方形线圈Ⅰ和Ⅱ,分别用相同材料,不同粗细的导线绕制(Ⅰ为细导线).两线圈在距磁场上界面h高处由静止开始自由下落,再进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈Ⅰ、Ⅱ落地时的速度大小分别为v1、v2,在磁场中运动时产生的热量分别为Q1、Q2.不计空气阻力,则( )