��Ŀ����
 ��ͼ��1����������ˮƽ�ٶ�V0����ƽ�н�����A��B����������MN���룬����������ѹUAB�ı仯������ͼ��2����ʾ����֪��������Ϊm�������Ϊe����ѹ����ΪT����ѹΪU0�������ӣ���������������֮��������������t=0ʱ�̽�������䣬��
��ͼ��1����������ˮƽ�ٶ�V0����ƽ�н�����A��B����������MN���룬����������ѹUAB�ı仯������ͼ��2����ʾ����֪��������Ϊm�������Ϊe����ѹ����ΪT����ѹΪU0�������ӣ���������������֮��������������t=0ʱ�̽�������䣬��| T |
| 2 |
�����������ӵ��˶���ˮƽ�������ֱ���������ֽ⣬ˮƽ�����������˶�����ֱ������ڵ糡�������������ٶ�Ϊ��ı���ֱ���˶��������ڲ�ͬʱ�����룬���Ը����˶�ѧ��ʽ��ʽ������Ҳ���Խ��ͼ������
����⣺�����Ӵ�t=0ʱ�̽�������䣬��
ʱ��ǡ���ܴӰ���ϱ�Ե�ɳ�������
ˮƽ���� L=v0t ��
��ֱ����
=
at2 ��
����t=
��a=
��
A��������t=
ʱ�̽�������䣬�ڰ������������ֱ�����˶����������̣�
-
ʱ������ȼ��٣�
-
Tʱ��������ȼ��ٺ��ȼ��٣���������Ϊ�ȱ��٣�
��ֱ��λ��Ϊ
y=
a(
)2+��a?
��
-
a(
) 2=
aT2
�ʵ��ӻ���Ϸ��������A����
B�������Ӵ�
ʱ�̽���糡������ֱ�����ȼ��ٺ����٣���ֱ��λ��Ϊ
y=
a��
��2+a?��
��?
=
aT2 ��
�ɢ٢ۢܵõ�y=
d��
�������Ӿ���������ڴ��Ϸ��������B��ȷ��
C������������ֱ�����ȼ��ٺ��ȼ����ټ����½�������ֱ��λ���п���Ϊ�㣬��C��ȷ��
D���ڴ�t=0ʱ�̵�t=
ʱ����һ��ʱ����������ĵ����У��糡���Ե�������Ϊ��W=eEy��eE
=
eU0����D����
��ѡBC��
| T |
| 2 |
ˮƽ���� L=v0t ��
��ֱ����
| d |
| 2 |
| 1 |
| 2 |
����t=
| T |
| 2 |
| eU0 |
| dm |
A��������t=
| T |
| 3 |
| T |
| 3 |
| T |
| 2 |
| T |
| 2 |
| 5 |
| 6 |
��ֱ��λ��Ϊ
y=
| 1 |
| 2 |
| T |
| 6 |
| T |
| 6 |
| T |
| 3 |
| 1 |
| 2 |
| T |
| 3 |
| 1 |
| 72 |
�ʵ��ӻ���Ϸ��������A����
B�������Ӵ�
| T |
| 4 |
y=
| 1 |
| 2 |
| T |
| 4 |
| T |
| 4 |
| T |
| 4 |
| 3 |
| 32 |
�ɢ٢ۢܵõ�y=
| 3 |
| 8 |
| d |
| 2 |
C������������ֱ�����ȼ��ٺ��ȼ����ټ����½�������ֱ��λ���п���Ϊ�㣬��C��ȷ��
D���ڴ�t=0ʱ�̵�t=
| T |
| 2 |
| d |
| 2 |
| 1 |
| 2 |
��ѡBC��
�����������е�����ˮƽ�������٣��ʾ����糡�����ʱ����һ���ģ���ֱ�����ڵ糡�����������������˶��������˶�ѧ��ʽ��ʽ��⼴�ɣ�

��ϰ��ϵ�д�
 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д�
�����Ŀ
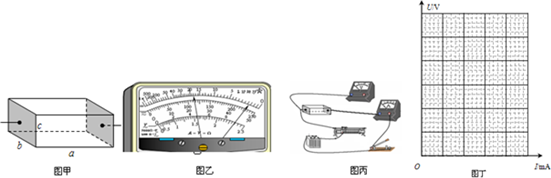
 A����ѡ��ģ��3-3��
A����ѡ��ģ��3-3��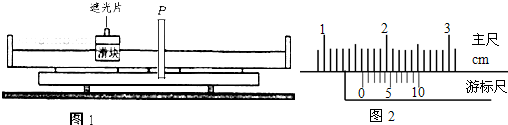
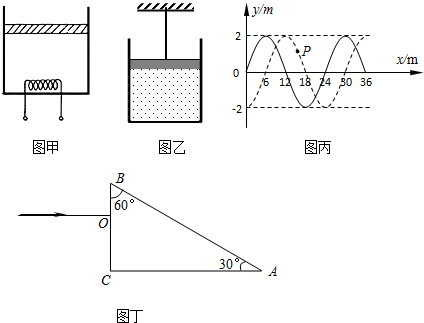
 ��1����ͼ��ʾ����ԭ�ӵ��ܼ�ͼ�����д�������n=3����̬����ԭ������ܼ�ԾǨ��������Ĺ����У�ֻ��һ����ʹij�����������ЧӦ�������ж���ȷ����
��1����ͼ��ʾ����ԭ�ӵ��ܼ�ͼ�����д�������n=3����̬����ԭ������ܼ�ԾǨ��������Ĺ����У�ֻ��һ����ʹij�����������ЧӦ�������ж���ȷ����

