题目内容
 如图所示,一平行板电容器与电源相连,从负极板上某处释放一个电子e,设其到达正极板的速度为v1,运动过程中加速度为a1,现将两板间距离增为原来的2倍,再从负极板处释放一电子,设其到达正极板的速度为v2,运动过程中加速度为a2,则( )
如图所示,一平行板电容器与电源相连,从负极板上某处释放一个电子e,设其到达正极板的速度为v1,运动过程中加速度为a1,现将两板间距离增为原来的2倍,再从负极板处释放一电子,设其到达正极板的速度为v2,运动过程中加速度为a2,则( )分析:平行板电容器之间形成匀强电场,电子在电场中做匀加速运动,根据牛顿第二定律求出加速度,根据动能定理求出速度即可求解.
解答:解:设电容器两端电压为U,距离为d,则:
E=
根据牛顿第二定律得:
a=
=
=
若将两板间距离增为原来的2倍,则:
=
故A错误,B正确;
电子从负极移动到正极的过程中运用动能定理得:
mv2=Ue
解得:v=
可见速度与极板间的距离无关,若将两板间距离增为原来的2倍,则其到达正极板的速度不变,即
=
故C错误,D正确.
故选BD
E=
| U |
| d |
根据牛顿第二定律得:
a=
| F |
| m |
| Ee |
| m |
| Ue |
| dm |
若将两板间距离增为原来的2倍,则:
| a1 |
| a2 |
| 2 |
| 1 |
故A错误,B正确;
电子从负极移动到正极的过程中运用动能定理得:
| 1 |
| 2 |
解得:v=
|
可见速度与极板间的距离无关,若将两板间距离增为原来的2倍,则其到达正极板的速度不变,即
| v1 |
| v2 |
| 1 |
| 1 |
故C错误,D正确.
故选BD
点评:本题主要考查了牛顿第二定律及动能定理的应用,知道电容器跟电源相连时,电容器两端电压不变.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
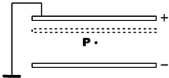 如图所示,一平行板电容器充电后与电源断开,正极板接地,在两极板间有一个负点电荷在P点恰好平衡.若用U表示两极板间的电压、E表示极板间的场强,并令负极板保持不动,而将正极板向下移到图中的虚线位置,则( )
如图所示,一平行板电容器充电后与电源断开,正极板接地,在两极板间有一个负点电荷在P点恰好平衡.若用U表示两极板间的电压、E表示极板间的场强,并令负极板保持不动,而将正极板向下移到图中的虚线位置,则( )| A、E增大,U减小 | B、E不变,U增大 | C、E增大,电荷有向上的加速度 | D、E不变,电荷电势能变小 |
 (2007?苏州二模)如图所示,一平行板电容器充电后与电源断开,负极板接地,在两极板间有一正电荷(电量很小)固定在P点.用E表示电容器两极板间的场强,U表示电容器两极板间的电压,ε表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( )
(2007?苏州二模)如图所示,一平行板电容器充电后与电源断开,负极板接地,在两极板间有一正电荷(电量很小)固定在P点.用E表示电容器两极板间的场强,U表示电容器两极板间的电压,ε表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( ) 如图所示,一平行板电容器充电后与电源断开,这时电容器的带电量为Q,P是电容器内一点,电容器的上板与大地相连,下列说法正确的是( )
如图所示,一平行板电容器充电后与电源断开,这时电容器的带电量为Q,P是电容器内一点,电容器的上板与大地相连,下列说法正确的是( ) 如图所示,一平行板电容器,上极板带正电下极板带负电,中间充满垂直于纸面向里的匀强磁场.一带电粒子a(不计重力)以一定的初速度由左边界的O点射入电容器,恰好沿直线从区域右边界的O′点(图中未标出)穿出.若撤去该区域内的磁场而其他条件均不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b( )
如图所示,一平行板电容器,上极板带正电下极板带负电,中间充满垂直于纸面向里的匀强磁场.一带电粒子a(不计重力)以一定的初速度由左边界的O点射入电容器,恰好沿直线从区域右边界的O′点(图中未标出)穿出.若撤去该区域内的磁场而其他条件均不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b( ) (2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )
(2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )