题目内容
（2013?湖北模拟）如图所示，由电阻不计的金属杆ab、cd构成的“V”字形对称光滑轨道，在轨道底部 由一小段光滑圆弧连接（其长度可忽略不计），bd间接有一定值电阻R，一根电阻不计 的导体棒在t=0时刻从ac端由静止开始下滑，整个装置处在方向竖直向上的匀强磁场 中．在导体棒第一次到达轨道右侧最高点的过程中，导体棒始终处于水平状态，现用v 表示导体棒速度的大小，则在下列四个v-t图象中，可能正确的是（ ）分析：由安培力公式求出导体棒受到的安培力，然后由牛顿第二定律求出导体棒的加速度，判断导体棒的运动状态，然后根据图象答题．
解答：解：导体棒从静止开始向下加速下滑，回路中产生感应电流，
导体棒受到沿导轨向上的安培力：F=BILcosθ=BL
cosθ=
，导体棒加速下滑，
安培力增大，导体棒下滑时的加速度a=
减小，
则导体棒下滑时做加速度减小的加速运动，
则导体棒下滑的运动过程是：一直做加速度减小的加速运动，
或先做加速度减小的加速运动后做匀速运动到底端；
然后导体棒滑上右侧轨道，在右侧轨道上安培力与运动方向相反，
所以导体棒做减速运动，其加速度为a=
，
加速度减小，一直到速度减小到零，由图象可知CD正确．
故选：CD．θ
导体棒受到沿导轨向上的安培力：F=BILcosθ=BL
| BLvcosθ |
| R |
| B2L2v(cosθ)2 |
| R |
安培力增大，导体棒下滑时的加速度a=
| mgsinθ-Fcosθ |
| m |
则导体棒下滑时做加速度减小的加速运动，
则导体棒下滑的运动过程是：一直做加速度减小的加速运动，
或先做加速度减小的加速运动后做匀速运动到底端；
然后导体棒滑上右侧轨道，在右侧轨道上安培力与运动方向相反，
所以导体棒做减速运动，其加速度为a=
| mgsinθ-Fcosθ |
| m |
加速度减小，一直到速度减小到零，由图象可知CD正确．
故选：CD．θ
点评：分析清楚导体棒的运动过程，求出导体棒受到的安培力、应用牛顿第二定律即可正确解题．
练习册系列答案
百分学生作业本题练王系列答案
相关题目
（2013?湖北模拟）在用打点计时器验证机械能守恒定律的实验中，使质量为m=1.00kg的重物自由下落，打点计时器在纸带上打出一系列的点，选取一条符合实验要求的纸带如图所示．O为第一个点，A、B、C为从合适位置开始选取连续点中的三个点．已知打点计时器每隔0.02s打一个点，当地的重力加速度为g=9.80m/s2，那么：
（2013?湖北模拟）如图所示，某同学骑电动车以 10m/s的速度匀速驶向路口，当行驶至距路口停车线20m处时，绿灯还有3s熄灭．而该同学在绿灯熄灭时刚好停在停车线处，则该同学运动的v-t图象可能是（ ）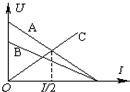
（2013?湖北模拟）如图所示，直线A为电源a的路端电压与电流的关系图象，直线B为电源b的路端电压与电流的关系图象，直线C为一个电阻R的两端电压与电流的关系图象．将这个电阻R分别接到a、b两电源上，那么（ ）
（2013?湖北模拟）一定质量的理想气体从状态A变化到状态B，再变化到状态C，其状态变化过程的p-V图象如图所示．已知该气体在状态A时的温度为27℃．则：
（2013?湖北模拟）如图所示，实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图．已知在t=0时刻，x=1.5m处的质点向y轴正方向运动．