题目内容
 如图所示,M、N 为一对处于匀强电场且与场强方向平行的荧光板,两板区域内的正中A点上有一静止的
如图所示,M、N 为一对处于匀强电场且与场强方向平行的荧光板,两板区域内的正中A点上有一静止的238 92 |
(l)写出
238 92 |
(2)求 M、N 板上的闪光点与 x 轴的距离之比:
| dM |
| dN |
分析:(1)根据电荷数守恒、质量数守恒写出衰变方程.
(2)根据动量守恒定律求出α粒子和反冲Th核的速度大小之比,从而得出运动的时间之比,结合牛顿第二定律和运动学公式求出 M、N 板上的闪光点与 x 轴的距离之比.
(2)根据动量守恒定律求出α粒子和反冲Th核的速度大小之比,从而得出运动的时间之比,结合牛顿第二定律和运动学公式求出 M、N 板上的闪光点与 x 轴的距离之比.
解答:解:(1)
U→
Th
He
(2)设α粒子的质量为m1、初速度为v1,Th核的质量为m2、速度大小为v2,它们沿x轴方向上的位移大小为s,从衰变到N、M板发出闪光的时间分别为t1、t2.
根据动量守恒定律m1v1=m2v2
故
=
t1=
,t2=
粒子在电场方向上的位移d=
at2=
M、N上的闪光点与x轴距离之比
=
=
=
=2632.5.
答:(1)衰变方程为
U→
Th
He
(2)M、N 板上的闪光点与 x 轴的距离之比:
=2632.5.
238 92 |
234 90 |
| + | 4 2 |
(2)设α粒子的质量为m1、初速度为v1,Th核的质量为m2、速度大小为v2,它们沿x轴方向上的位移大小为s,从衰变到N、M板发出闪光的时间分别为t1、t2.
根据动量守恒定律m1v1=m2v2
故
| v1 |
| v2 |
| m2 |
| m1 |
t1=
| s |
| v1 |
| s |
| v2 |
粒子在电场方向上的位移d=
| 1 |
| 2 |
| qEs2 |
| 2mv2 |
M、N上的闪光点与x轴距离之比
| dM |
| dN |
| q2m1v12 |
| q1m2v22 |
| q2m2 |
| q1m1 |
| 90×234 |
| 2×4 |
答:(1)衰变方程为
238 92 |
234 90 |
| + | 4 2 |
(2)M、N 板上的闪光点与 x 轴的距离之比:
| dM |
| dN |
点评:解决本题的关键知道α粒子和反冲Th做类平抛运动,结合动量守恒定律、牛顿第二定律和运动学公式综合求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
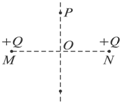 如图所示,M、N为两个等量同种电荷,在其连线的中垂线上的P点放一静止的点电荷q(负电荷),不计重力,下列说法中正确的是( )
如图所示,M、N为两个等量同种电荷,在其连线的中垂线上的P点放一静止的点电荷q(负电荷),不计重力,下列说法中正确的是( )| A、点电荷在从P到O的过程中,加速度越来越大,速度也越来越大 | B、点电荷在从P到O的过程中,加速度越来越小,速度越来越大 | C、点电荷运动到O点时加速度为零,速度达最大值 | D、点电荷越过O点后,速度越来越小,加速度越来越大,直到粒子速度为零 |
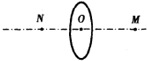 如图所示,M、N为均匀带电的细圆环轴线上的两点,O为圆环圆心,M点与O的距离大于N点与O的距离.若圆环所带电荷为正电荷,无穷远处电势为零,下列说法正确的是( )
如图所示,M、N为均匀带电的细圆环轴线上的两点,O为圆环圆心,M点与O的距离大于N点与O的距离.若圆环所带电荷为正电荷,无穷远处电势为零,下列说法正确的是( )| A、O点电势为零 | B、N点电势比点M高 | C、M点电场强度比N点小 | D、O点电场强度比N点大 |
 如图所示,M、N为两块水平放置的平行金属板,两板长度均为L=4cm,两板间距离d=3.2cm,两板间电压U=480V.在金属板右侧有垂直纸面的匀强磁场,P、Q两条竖直线为匀强磁场的边界,P、Q间距离s=3cm.一个质量m=1.6×10-26Kg、电荷量q=8.0×10-19C的负电荷(不计重力),以速度V0=2.0×105m/s从金属板左侧沿中线射入两板间,从金属板右侧飞出后又进入PQ间的匀强磁场中,最后从磁场右边界水平飞出.试求:
如图所示,M、N为两块水平放置的平行金属板,两板长度均为L=4cm,两板间距离d=3.2cm,两板间电压U=480V.在金属板右侧有垂直纸面的匀强磁场,P、Q两条竖直线为匀强磁场的边界,P、Q间距离s=3cm.一个质量m=1.6×10-26Kg、电荷量q=8.0×10-19C的负电荷(不计重力),以速度V0=2.0×105m/s从金属板左侧沿中线射入两板间,从金属板右侧飞出后又进入PQ间的匀强磁场中,最后从磁场右边界水平飞出.试求: 如图所示,M、N为电场中两个等势面,PQ直线是其中的一条电场线,则下列说法中正确的是( )
如图所示,M、N为电场中两个等势面,PQ直线是其中的一条电场线,则下列说法中正确的是( )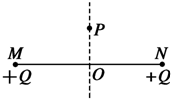 如图所示,M、N为两个固定的等量同种正电荷,在其连线的中垂线上的P点放一个静止的负电荷(重力不计),下列说法中正确的是( )
如图所示,M、N为两个固定的等量同种正电荷,在其连线的中垂线上的P点放一个静止的负电荷(重力不计),下列说法中正确的是( )