题目内容
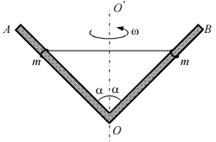
 如图,V形细杆AOB能绕其对称轴OO’转动,OO’沿竖直方向,V形杆的两臂与转轴间的夹角均为α=45°.两质量均为m=0.1kg的小环,分别套在V形杆的两臂上,并用长为L=1.2m、能承受最大拉力Fmax=4.5N的轻质细线连接.环与臂间的最大静摩擦力等于两者间弹力的0.2倍.当杆以角速度ω转动时,细线始终处于水平状态,取g=10m/s2.
如图,V形细杆AOB能绕其对称轴OO’转动,OO’沿竖直方向,V形杆的两臂与转轴间的夹角均为α=45°.两质量均为m=0.1kg的小环,分别套在V形杆的两臂上,并用长为L=1.2m、能承受最大拉力Fmax=4.5N的轻质细线连接.环与臂间的最大静摩擦力等于两者间弹力的0.2倍.当杆以角速度ω转动时,细线始终处于水平状态,取g=10m/s2.(1)求杆转动角速度ω的最小值;
(2)将杆的角速度从(1)问中求得的最小值开始缓慢增大,直到细线断裂,写出此过程中细线拉力随角速度变化的函数关系式.
分析:(1)角速度最小时,fmax沿杆向上,此时绳处于松弛状态,由竖直方向由平衡条件列式及水平方向根据牛顿第二定律列式即可求解;
(2)当fmax沿杆向下时,绳仍处于松弛状态,由竖直方向由平衡条件列式及水平方向根据牛顿第二定律列式即可求解角速度,此后,拉力随ω的增大而变大,当细线拉力刚达到最大时,求出最大角速度,进而求出拉力.
(2)当fmax沿杆向下时,绳仍处于松弛状态,由竖直方向由平衡条件列式及水平方向根据牛顿第二定律列式即可求解角速度,此后,拉力随ω的增大而变大,当细线拉力刚达到最大时,求出最大角速度,进而求出拉力.
解答:解:(1)角速度最小时,fmax沿杆向上,此时绳处于松弛状态则
竖直方向由平衡条件得FNsin45°+fmaxcos45°=mg,
水平方向由牛顿第二定律得FNcos45°+fmaxsin45°=mω12r,
且fmax=0.2FN,r=
,
解得ω1=
≈3.33rad/s
(2)当fmax沿杆向下时,绳仍处于松弛状态,有
竖直方向由平衡条件得FNsin45°=fmaxcos45°+mg,
水平方向由牛顿第二定律得FNcos45°+fmaxsin45°=mω22r,
解得ω2=5rad/s
此后,拉力随ω的增大而变大,当细线拉力刚达到最大时,有
FNsin45°-fmaxcos45°=mg
Fmax+FNcos45°-fmaxsin45°=mω32r,
解得ω3=10rad/s
因此在ω2~ω3间,F拉=mω2r-FNcos45°+fmaxsin45°
所以拉力随角速度的函数关系式为:F拉=0(
rad/s≤ω≤5rad/s);F拉=0.06ω2-1.5(5rad/s<ω<10rad/s)
答:(1)杆转动角速度ω的最小值为3.33rad/s;
(2)将杆的角速度从(1)问中求得的最小值开始缓慢增大,直到细线断裂,此过程中细线拉力随角速度变化的函数关系式为
F拉=0(
rad/s≤ω≤5rad/s);F拉=0.06ω2-1.5(5rad/s<ω<10rad/s).
竖直方向由平衡条件得FNsin45°+fmaxcos45°=mg,
水平方向由牛顿第二定律得FNcos45°+fmaxsin45°=mω12r,
且fmax=0.2FN,r=
| l |
| 2 |
解得ω1=
| 10 |
| 3 |
(2)当fmax沿杆向下时,绳仍处于松弛状态,有
竖直方向由平衡条件得FNsin45°=fmaxcos45°+mg,
水平方向由牛顿第二定律得FNcos45°+fmaxsin45°=mω22r,
解得ω2=5rad/s
此后,拉力随ω的增大而变大,当细线拉力刚达到最大时,有
FNsin45°-fmaxcos45°=mg
Fmax+FNcos45°-fmaxsin45°=mω32r,
解得ω3=10rad/s
因此在ω2~ω3间,F拉=mω2r-FNcos45°+fmaxsin45°
所以拉力随角速度的函数关系式为:F拉=0(
| 10 |
| 3 |
答:(1)杆转动角速度ω的最小值为3.33rad/s;
(2)将杆的角速度从(1)问中求得的最小值开始缓慢增大,直到细线断裂,此过程中细线拉力随角速度变化的函数关系式为
F拉=0(
| 10 |
| 3 |
点评:本题的关键是能对圆环进行受力分析,根据竖直方向由平衡条件列式及水平方向牛顿第二定律列式求解,难度适中.

练习册系列答案
相关题目
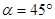 。两质量均为
。两质量均为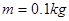 的小环,分别套在V形杆的两臂上,并用长为
的小环,分别套在V形杆的两臂上,并用长为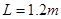 、能承受最大拉力
、能承受最大拉力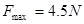 的轻质细线连结。环与臂间的最大静摩擦力等于两者间弹力的0.2倍。当杆以角速度
的轻质细线连结。环与臂间的最大静摩擦力等于两者间弹力的0.2倍。当杆以角速度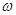 转动时,细线始终处于水平状态,取
转动时,细线始终处于水平状态,取 。]
。]
 。两质量均为
。两质量均为 的小环,分别套在V形杆的两臂上,并用长为
的小环,分别套在V形杆的两臂上,并用长为 、能承受最大拉力
、能承受最大拉力 的轻质细线连结。环与臂间的最大静摩擦力等于两者间弹力的0.2倍。当杆以角速度
的轻质细线连结。环与臂间的最大静摩擦力等于两者间弹力的0.2倍。当杆以角速度 转动时,细线始终处于水平状态,取
转动时,细线始终处于水平状态,取 。]
。] 
