��Ŀ����
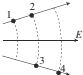
����Ŀ����ͼ��ʾ��M��ˮƽ���õİ뾶�㹻���Բ�̣��ƹ���Բ�ĵ���ֱ��OO������ת�����涨����Բ��Oˮƽ����Ϊx�����������Բ��O���Ϸ��������Ϊh����һ�����ڼ�ϵ�ˮ����������t=0ʱ�̿�ʼ�洫�ʹ�����x��ƽ�еķ���������ֱ���˶����ٶȴ�СΪv����֪������t=0ʱ�̵��µ�һ��ˮ���Ժ�ÿ��ǰһ��ˮ�պ��䵽������ʱ�ٵ�һ��ˮ����
��1��Ҫʹÿһ��ˮ�������ϵ���㶼λ��ͬһֱ���ϣ�Բ��ת���Ľ��ٶ���ӦΪ���
��2���ڶ���ˮ�������ˮ�������������������x��

���𰸡���1��![]() ��2��
��2��![]()
����������1��ˮ������ֱ���������������˶������� ![]() ����
����![]()
Ҫʹÿһ��ˮ��Բ�����ϵ���㶼λ��ͬһ��ֱ���ϣ�����������ˮ������ʱ���ڣ�Բ��ת���ĽǶ�Ϊn�������Խ��ٶ�Ϊ�� ![]() ��
��
��2���ڶ���ˮ����Բ���ϵ�ˮƽλ��Ϊ�� ![]()
������ˮ��Բ���ϵ�ˮƽλ��Ϊ�� ![]()
���ڶ���ˮ�������ˮ�������ϵ����λ��ͬһֱ����Բ�ĵ�����ʱ�����ľ������
�� ![]() ��
��

��ϰ��ϵ�д�
�����Ŀ