题目内容
 质量分别为2m和m的A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )
质量分别为2m和m的A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )A.F1和F2大小相等
B.F1和F2对A、B做功之比为2:1
C.A、B所受摩擦力大小相等
D.全过程中摩擦力对A、B做功之比为1:2
【答案】分析:根据速度与时间的图象可知,各段运动的位移关系及之比,同时由牛顿第二定律可得匀减速运动的加速度之比;再由动能定理可得出拉力、摩擦力的关系,及它们的做功关系.
解答:解:由速度与时间图象可知,两个匀减速运动的加速度之比为1:2;由牛顿第二定律可知:A、B的质量关系是2:1,则A、B受摩擦力大小1:1,故C正确;
由速度与时间图象可知,A、B两物体加速与减速的位移相等,且匀加速运动位移之比1:2,匀减速运动的位移之比2:1,由动能定理可得:A物体的拉力与摩擦力的关系,F1?X-f1?3X=0-0;B物体的拉力与摩擦力的关系,F2?2X-f2?3X=0-0,因此可得:F1=3f1, ,f1=f2,所以F1=2F2.全过程中摩擦力对A、B做功相等.;F1、F2对A、B做功之大小相等.故A、B、D错误.
,f1=f2,所以F1=2F2.全过程中摩擦力对A、B做功相等.;F1、F2对A、B做功之大小相等.故A、B、D错误.
故选C.
点评:解决本题的关键通过图象得出匀加速运动和匀减速运动的加速度,根据牛顿第二定律,得出两个力的大小之比,以及知道速度-时间图线与时间轴所围成的面积表示位移,并运用动能定理.
解答:解:由速度与时间图象可知,两个匀减速运动的加速度之比为1:2;由牛顿第二定律可知:A、B的质量关系是2:1,则A、B受摩擦力大小1:1,故C正确;
由速度与时间图象可知,A、B两物体加速与减速的位移相等,且匀加速运动位移之比1:2,匀减速运动的位移之比2:1,由动能定理可得:A物体的拉力与摩擦力的关系,F1?X-f1?3X=0-0;B物体的拉力与摩擦力的关系,F2?2X-f2?3X=0-0,因此可得:F1=3f1,
 ,f1=f2,所以F1=2F2.全过程中摩擦力对A、B做功相等.;F1、F2对A、B做功之大小相等.故A、B、D错误.
,f1=f2,所以F1=2F2.全过程中摩擦力对A、B做功相等.;F1、F2对A、B做功之大小相等.故A、B、D错误.故选C.
点评:解决本题的关键通过图象得出匀加速运动和匀减速运动的加速度,根据牛顿第二定律,得出两个力的大小之比,以及知道速度-时间图线与时间轴所围成的面积表示位移,并运用动能定理.

练习册系列答案
相关题目
如图所示,倾角α=30°的等腰三角形斜面固定在水平面上,质量分别为2m和m的A、B 两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮质量和摩擦).已知A滑块和左侧斜面的 动摩擦因数μ=
,B与右侧斜面间光滑接触.且A、B均处于静止状态,则A与斜面间的摩擦力fA的大小和方向为( )
| ||
| 2 |

A、fA=
| ||
B、fA=
| ||
C、fA=
| ||
| D、fA=mg,沿斜面向上 |
 如图所示,两光滑斜面的倾角分别为30°和45°,质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静止释放;若交换两滑块位置,再由静止释放,则在上述两种情形中,下列说法不正确的有( )
如图所示,两光滑斜面的倾角分别为30°和45°,质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静止释放;若交换两滑块位置,再由静止释放,则在上述两种情形中,下列说法不正确的有( ) 如图所示,质量分别为2m和m的两个物体A和B,用轻弹簧连在一起,放在光滑的水平面上.在水平拉力F的作用下,两物体相对静止一起向右做匀加速运动,则弹簧的弹力的大小为
如图所示,质量分别为2m和m的两个物体A和B,用轻弹簧连在一起,放在光滑的水平面上.在水平拉力F的作用下,两物体相对静止一起向右做匀加速运动,则弹簧的弹力的大小为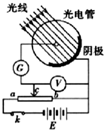 (1)用如图所示的装置研究光电效应现象,用光子能量为2.5eV的光照射到光电管上时,电流表G示数不为0,移动变阻器的触点c,当电压表的示数大于或等于时0.7V,电流表示数为0,则
(1)用如图所示的装置研究光电效应现象,用光子能量为2.5eV的光照射到光电管上时,电流表G示数不为0,移动变阻器的触点c,当电压表的示数大于或等于时0.7V,电流表示数为0,则