题目内容
如图所示,AB、BC均为轻杆,处在同一竖直平面内,AB杆高为h. A、B、C三处均用铰接连接,其中A、C两点在同一水平面上,BC杆与水平面夹角为30°.一个质量为m的小球穿在BC杆上,并静止在BC杆底端C处,不计一切摩擦.现在对小球施加一个水平向左的恒力F=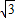 mg,则当小球运动到BC杆的中点时,它的速度大小为 ,此时AB杆对B处铰链的作用力大小为 .
mg,则当小球运动到BC杆的中点时,它的速度大小为 ,此时AB杆对B处铰链的作用力大小为 .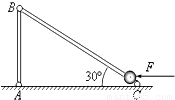
【答案】分析:对小球进行受力分析求出小球的加速度,再根据匀加速直线运动位移速度公式即可求解小球运动到BC杆的中点时的速度,以C为转轴,根据力矩平衡列方程求解此时AB杆对B处铰链的作用力大小.
解答:解:对小球进行受力分析,如图所示:
 根据牛顿第二定律得:
根据牛顿第二定律得:
ma=Fcos30°-mgsin30°=mg
所以a=g
则当小球运动到BC杆的中点时,运动的位移为: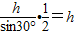
根据匀加速直线运动位移速度公式得: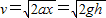
当小球运动到BC杆的中点时,小球对杆子的作用力方向垂直于杆子向下,根据几何关系得大小:N=mgcos30°=
此时BC杆相当于绕C点转动的杠杆,根据杠杆平衡原理得:
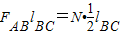 +F
+F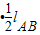
解得:FAB=mg
故答案为: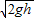 ,mg
,mg
点评:本题主要考查了牛顿第二定律及杠杆原理的应用,关键是受力分析,难度适中.
解答:解:对小球进行受力分析,如图所示:
 根据牛顿第二定律得:
根据牛顿第二定律得:ma=Fcos30°-mgsin30°=mg
所以a=g
则当小球运动到BC杆的中点时,运动的位移为:
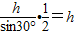
根据匀加速直线运动位移速度公式得:
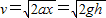
当小球运动到BC杆的中点时,小球对杆子的作用力方向垂直于杆子向下,根据几何关系得大小:N=mgcos30°=

此时BC杆相当于绕C点转动的杠杆,根据杠杆平衡原理得:
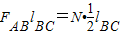 +F
+F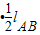
解得:FAB=mg
故答案为:
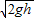 ,mg
,mg点评:本题主要考查了牛顿第二定律及杠杆原理的应用,关键是受力分析,难度适中.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 一定质量的理想气体压强p与热力学温度T的关系图象如图所示,AB、BC分别与p轴和T轴平行,气体在状态A时的压强为p0、体积为V0,在状态B时的压强为2p0,则气体在状态B时的体积为
一定质量的理想气体压强p与热力学温度T的关系图象如图所示,AB、BC分别与p轴和T轴平行,气体在状态A时的压强为p0、体积为V0,在状态B时的压强为2p0,则气体在状态B时的体积为 (2010?上海)一定量的理想气体的状态经历了如图所示的ab、bc、cd、da四个过程.其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da和bc平行.则气体体积在( )
(2010?上海)一定量的理想气体的状态经历了如图所示的ab、bc、cd、da四个过程.其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da和bc平行.则气体体积在( ) (2011?静安区二模)一定质量理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中ab的反向延长线通过原点,da与横轴平行,bc垂直与纵轴平行,cd与ab平行,则气体压强在( )
(2011?静安区二模)一定质量理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中ab的反向延长线通过原点,da与横轴平行,bc垂直与纵轴平行,cd与ab平行,则气体压强在( ) (2010?普陀区一模)如图所示,AB、BC均为轻杆,处在同一竖直平面内,AB杆高为h.A、B、C三处均用铰接连接,其中A、C两点在同一水平面上,BC杆与水平面夹角为30°.一个质量为m的小球穿在BC杆上,并静止在BC杆底端C处,不计一切摩擦.现在对小球施加一个水平向左的恒力F=mg,则当小球运动到BC杆的中点时,它的速度大小为
(2010?普陀区一模)如图所示,AB、BC均为轻杆,处在同一竖直平面内,AB杆高为h.A、B、C三处均用铰接连接,其中A、C两点在同一水平面上,BC杆与水平面夹角为30°.一个质量为m的小球穿在BC杆上,并静止在BC杆底端C处,不计一切摩擦.现在对小球施加一个水平向左的恒力F=mg,则当小球运动到BC杆的中点时,它的速度大小为 如图所示,AB和BC是两段半径、长度及粗糙程度均相同的圆弧形路面,它们在B处相切平滑连在一起,且A、B、c在同一水平面上.一小物块以初速度v0从A端沿路面滑到C端时的速度大小为v1;而以同样大小的初速度v0从c端沿路面滑到A端时的速度大小为v2.则( )
如图所示,AB和BC是两段半径、长度及粗糙程度均相同的圆弧形路面,它们在B处相切平滑连在一起,且A、B、c在同一水平面上.一小物块以初速度v0从A端沿路面滑到C端时的速度大小为v1;而以同样大小的初速度v0从c端沿路面滑到A端时的速度大小为v2.则( )