题目内容
有三个质量相等,半径均为r的圆柱体,同置于一块圆弧曲面上,整个装置如图所示.为了使下面两下圆柱体不致分开,则圆弧曲面的半径R最大是多少?(所有摩擦均不计)
【答案】分析:设圆弧曲面对小球支持力的方向与竖直方向夹角为α,先对整体受力分析,求出圆弧曲面对球的支持力,考虑临界状态,当下面两球之间弹力为0时半径取极值,再对下面任一小球受力分析,三力平衡,正交分解,列方程可求.
解答:解:设圆弧曲面对小球支持力的方向与竖直方向夹角为α,对整体受力分析,
有:
2Ncosα=3mg,得:N= ①
①
对最上面一个小球进行受力分析,有:2Fcos30°=mg ②,
对下面的其中一个小球受力分析,有:Ncosα=Fcos30°+mg ③
cosα= ④
④
联立①②③④得:R=3 r+r
r+r
答:圆弧曲面的半径R最大是3 r+r.
r+r.
点评:隔离法和整体法受力分析后,根据平衡条件列方程求解即可,难点是出现了三个物体,研究对象较多.
解答:解:设圆弧曲面对小球支持力的方向与竖直方向夹角为α,对整体受力分析,
有:
2Ncosα=3mg,得:N=
 ①
①对最上面一个小球进行受力分析,有:2Fcos30°=mg ②,
对下面的其中一个小球受力分析,有:Ncosα=Fcos30°+mg ③
cosα=
 ④
④联立①②③④得:R=3
 r+r
r+r答:圆弧曲面的半径R最大是3
 r+r.
r+r.点评:隔离法和整体法受力分析后,根据平衡条件列方程求解即可,难点是出现了三个物体,研究对象较多.

练习册系列答案
相关题目
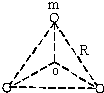 宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( )
宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( )| A、每颗星做圆周运动的半径为等边三角形的边长R | B、每颗星做圆周运动的加速度与三星的质量无关 | C、利用所给物理量不能求出每颗星做圆周运动的线速度大小 | D、利用所给物理量能求出每颗星做圆周运动的周期 |
 有三个质量相等,半径均为r的圆柱体,同置于一块圆弧曲面上,整个装置如图所示.为了使下面两下圆柱体不致分开,则圆弧曲面的半径R最大是多少?(所有摩擦均不计)
有三个质量相等,半径均为r的圆柱体,同置于一块圆弧曲面上,整个装置如图所示.为了使下面两下圆柱体不致分开,则圆弧曲面的半径R最大是多少?(所有摩擦均不计)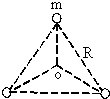 宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( )
宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( ) 有三个质量相等,半径均为r的圆柱体,同置于一块圆弧曲面上,整个装置如图所示.为了使下面两下圆柱体不致分开,则圆弧曲面的半径R最大是多少?(所有摩擦均不计)
有三个质量相等,半径均为r的圆柱体,同置于一块圆弧曲面上,整个装置如图所示.为了使下面两下圆柱体不致分开,则圆弧曲面的半径R最大是多少?(所有摩擦均不计)