题目内容
如图4-7所示，两根轻绳同系一个质量m=0.1kg的小球，两绳的另一端分别固定在轴上的A、B两处，上面绳AC长L=2m，当两绳都拉直时，与轴的夹角分别为30°和45°，求当小球随轴一起在水平面内做匀速圆周运动角速度为ω=4rad/s时，上下两轻绳拉力各为多少？
①
②
代入数据得：
，
要使BC绳有拉力，应有ω>ω1，当AC绳恰被拉直，但其拉力T1恰为零，设此时角速度为ω2，BC绳拉力为T2，则有
③
T2sin45°=m
LACsin30°④
代入数据得：ω2=3.16rad/s。要使AC绳有拉力，必须ω<ω2，依题意ω=4rad/s>ω2，故AC绳已无拉力，AC绳是松驰状态，BC绳与杆的夹角θ>45°，对小球有：
T2cosθ=m ω2LBCsin θ ⑤
而LACsin30°=LBCsin45° LBC=
m ⑥
由⑤、⑥可解得 
；
练习册系列答案
相关题目
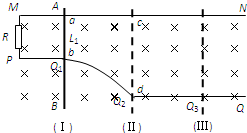如图所示，两根不计电阻的金属导线MN与PQ 放在水平面内，MN是直导线，PQ的PQ1段是直导线，Q1Q2段是弧形导线，Q2Q3段是直导线，MN、PQ1、Q2Q3相互平行．M、P间接入一个阻值R=0.25Ω的电阻．质量m=1.0kg、不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动，金属棒始终垂直于MN，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向竖直向下．金属棒处于位置（I）时，给金属棒一向右的初速度v1=4 m/s，同时给一方向水平向右F1=3N的外力，使金属棒向右做匀减速直线运动；当金属棒运动到位置（Ⅱ）时，外力方向不变，改变大小，使金属棒向右做匀速直线运动2s到达位置（Ⅲ）．已知金属棒在位置（I）时，与MN、Q1Q2相接触于a、b两点，a、b的间距L1=1 m；金属棒在位置（Ⅱ）时，棒与MN、Q1Q2相接触于c、d两点；位置（I）到位置（Ⅱ）的距离为7.5m．求：
如图所示，两根不计电阻的金属导线MN与PQ 放在水平面内，MN是直导线，PQ的PQ1段是直导线，Q1Q2段是弧形导线，Q2Q3段是直导线，MN、PQ1、Q2Q3相互平行，M、P间接入一个阻值R=0.25Ω的电阻．一根质量为1.0kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动，金属棒始终垂直于MN，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向竖直向下．金属棒处于位置（I）时，给金属棒一个向右的速度v1=4 m/s，同时方向水平向右的外力F1=3N作用在金属棒上使金属棒向右做匀减速直线运动；当金属棒运动到位置（Ⅱ）时，外力方向不变，大小变为F2，金属棒向右做匀速直线运动，经过时间t=2s到达位置（Ⅲ）．金属棒在位置（I）时，与MN、Q1Q2相接触于a、b两点，a、b的间距L1=1 m，金属棒在位置（Ⅱ）时，棒与MN、Q1Q2相接触于c、d两点．已知s1=7.5m．求：
为（ ）? 
? B.
? C.
? D.
= k
，（d
表示导体元段的方向沿电流的方向、
为导体元段到考查点的方向矢量）；或用大小关系式dB = k
结合安培定则寻求方向亦可。其中 k = 1.0×10?7N/A2 。应用毕萨定律再结合矢量叠加原理，可以求解任何形状导线在任何位置激发的磁感强度。
；
；
= I
；或表达为大小关系式 F = BILsinθ再结合“左手定则”解决方向问题（θ为B与L的夹角）。
= q
，或展开为f = qvBsinθ再结合左、右手定则确定方向（其中θ为
与
的夹角）。安培力是大量带电粒子所受洛仑兹力的宏观体现。
总垂直
与
确定的平面，故
总垂直
，只能起到改变速度方向的作用。结论：洛仑兹力可对带电粒子形成冲量，却不可能做功。或：洛仑兹力可使带电粒子的动量发生改变却不能使其动能发生改变。
⊥
时，匀速圆周运动，半径r = 
，周期T = 
与
成一般夹角θ时，做等螺距螺旋运动，半径r = 
，螺距d = 
分解…（过程从略）。
分解（成垂直速度分量B2和平行速度分量B1 ，如图9-7所示），粒子的运动情形似乎就不一样了——在垂直B2的平面内做圆周运动？
=
= 2πRf