题目内容
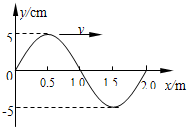
 如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题:
如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题:(1)画出x=2.0m处质点的振动图象;
(2)求出x=2.5m处质点在0~4.5s内通过的路程及t=4.5s时的位移.
(3)此时A点的纵坐标为2cm,试求从图示时刻开始经过多少时间A点第一次出现波峰?
分析:(1)由波动图象读出振幅和波长,求出周期.t=0时刻,x=2.0m处质点经过平衡位置向下振动,画出振动图象.
(2)根据时间4.5s与周期的关系,分析x=2.5m处质点在0~4.5s内通过的路程及t=4.5s时的位移.质点在一个周期内通过的路程是四个振幅.
(3)写出波动方程,求出A点的横坐标.当A左侧最近的波峰状态传到A点时,A点第一次出现波峰,根据距离与波速之比求出时间.
(2)根据时间4.5s与周期的关系,分析x=2.5m处质点在0~4.5s内通过的路程及t=4.5s时的位移.质点在一个周期内通过的路程是四个振幅.
(3)写出波动方程,求出A点的横坐标.当A左侧最近的波峰状态传到A点时,A点第一次出现波峰,根据距离与波速之比求出时间.
解答:解:(1)由波动图象读出振幅A=4cm,波长λ=2m,则周期为:T=
=
s=1s
t=0时刻,x=2.0m处质点经过平衡位置向 下振动,其振动图象如图.
下振动,其振动图象如图.
(2)t=4.5s=4.5T,x=2.5m处质点在0~4.5s内通过的路程为:
S=4.5×4A=18×4cm=72cm
t=4.5s时x=2.5m处质点到波谷,则t=4.5s时的位移为:y=-4cm.
(3)该波的方程为y=Asin
x(cm)=4sinπx(cm),当y=2cm时,x=
cm,A左侧最近的波峰状态离A点的距离为:
△x=1.5cm+
cm=
cm
从图示时刻开始 A点第一次出现波峰的时间为:
t=
=
s=0.83s.
答:(1)画出x=2.0m处质点的振动图象如图;
(2)x=2.5m处质点在0~4.5s内通过的路程为72cm,t=4.5s时的位移为-4cm.
(3)从图示时刻开始 经过0.83s时间A点第一次出现波峰.
| λ |
| v |
| 2 |
| 2 |
t=0时刻,x=2.0m处质点经过平衡位置向
 下振动,其振动图象如图.
下振动,其振动图象如图.(2)t=4.5s=4.5T,x=2.5m处质点在0~4.5s内通过的路程为:
S=4.5×4A=18×4cm=72cm
t=4.5s时x=2.5m处质点到波谷,则t=4.5s时的位移为:y=-4cm.
(3)该波的方程为y=Asin
| 2π |
| 2 |
| 1 |
| 6 |
△x=1.5cm+
| 1 |
| 6 |
| 5 |
| 3 |
从图示时刻开始 A点第一次出现波峰的时间为:
t=
| △x |
| v |
| ||
| 2 |
答:(1)画出x=2.0m处质点的振动图象如图;
(2)x=2.5m处质点在0~4.5s内通过的路程为72cm,t=4.5s时的位移为-4cm.
(3)从图示时刻开始 经过0.83s时间A点第一次出现波峰.
点评:本题首先考查把握质点的振动与波动之间的联系,运用波形的平移求A第一次形成波峰的时间是基本方法.

练习册系列答案
相关题目
 (2009?徐州二模)(选修模块3-4)
(2009?徐州二模)(选修模块3-4) °.已知这种玻璃的折射率n=
°.已知这种玻璃的折射率n= (2012?南京模拟)如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,波的传播速度v=2m/s,试求:
(2012?南京模拟)如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,波的传播速度v=2m/s,试求: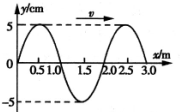 如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题:
如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题: