题目内容
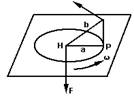
如图所示,在水平固定的光滑平板上,有一质量为M的质点P,与穿过中央小孔H的轻绳一端连着.平板与小孔是光滑的,用手拉着绳子下端,使质点做半径为a、角速度为ω1的匀速圆周运动.若绳子迅速放松至某一长度b而拉紧,质点就能在以半径为b的圆周上做匀速圆周运动.求质点由半径a到b所需的时间及质点在半径为b的圆周上运动的角速度.
【答案】
(1)t=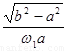 (2)ωb=
(2)ωb=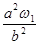
【解析】质点在半径为a的圆周上以角速度ω1做匀速圆周运动,其线速度为: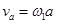
突然松绳后,向心力消失,质点沿切线方向飞出,以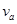 的速度做匀速直线运动,
的速度做匀速直线运动,
直到质点m距O点的距离为B时,绳子将被拉直.如图所示,做出质点这一过程的俯视图,
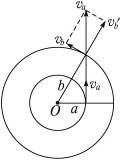
则质点在匀速直线运动中的位移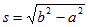
因此质点m由半径A到B所需的时间为: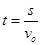 =
=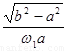 .
.
当线刚被拉直时,质点的速度为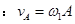
把这一速度分解为垂直于绳的速度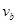 和沿绳的速度
和沿绳的速度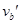 ,
,
在绳绷紧的过程中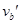 减为零,质点就以
减为零,质点就以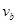 沿着半径为B的圆周做匀速圆周运动.
沿着半径为B的圆周做匀速圆周运动.
设其角速度为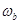 ,根据相似三角形得:
,根据相似三角形得: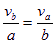 ,即
,即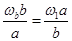 ,
,
则质点沿半径为B的圆周做匀速圆周运动的角速度为:ωb=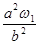 .
.
思路分析:质点先做半径为a的圆周上以角速度ω1做匀速圆周运动,求出线速度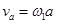 ,绳子松开之后以
,绳子松开之后以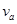 的速度做匀速直线运动,绳子将被拉直是求出位移
的速度做匀速直线运动,绳子将被拉直是求出位移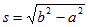 。根据匀速直线求出时间,被拉直的瞬间,沿绳速度减为零,只剩下垂直与绳的速度,根据三角形相似:
。根据匀速直线求出时间,被拉直的瞬间,沿绳速度减为零,只剩下垂直与绳的速度,根据三角形相似: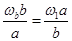 ,求出以半径为B做圆周运动时的角速度。
,求出以半径为B做圆周运动时的角速度。
试题点评:本题考查利用圆周运动、离心运动以及运动的合成和分解等知识综合分析、处理问题的能力.要注意分析质点的运动过程,要明确绳松开后,向心力突然消失,质点沿切线方向飞出,沿光滑平板做匀速直线运动,这是该题的易错点

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图所示,在水平固定的筒形绝热气缸中,用绝热的活塞封闭一部分气体,活塞与气缸之间无摩擦且不漏气.外界大气压强恒为p0,气体温度为27℃时,活塞与汽缸底相距45cm.用一个电阻丝R给气体加热,活塞将会缓慢移动,使气缸内气体温度升高到77℃.求:
如图所示,在水平固定的筒形绝热气缸中,用绝热的活塞封闭一部分气体,活塞与气缸之间无摩擦且不漏气.外界大气压强恒为p0,气体温度为27℃时,活塞与汽缸底相距45cm.用一个电阻丝R给气体加热,活塞将会缓慢移动,使气缸内气体温度升高到77℃.求: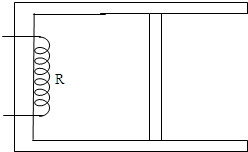 (选修模块3-3)
(选修模块3-3) 如图所示,在水平固定的筒形绝热气缸中,用绝热的活塞封闭一部分气体.活塞的横截面积为0.2m2,外界大气压强为105Pa,气体温度为27℃.活塞与气缸之间无摩擦间不漏气.用一个电阻丝R给气体加热,活塞将会缓慢移动当气缸内温度升高到77℃时,活塞移动了7.5cm.已知被封闭气体的温度每升高1℃,其内能增加74.8J,求电阻丝对气体提供的热量为多少?
如图所示,在水平固定的筒形绝热气缸中,用绝热的活塞封闭一部分气体.活塞的横截面积为0.2m2,外界大气压强为105Pa,气体温度为27℃.活塞与气缸之间无摩擦间不漏气.用一个电阻丝R给气体加热,活塞将会缓慢移动当气缸内温度升高到77℃时,活塞移动了7.5cm.已知被封闭气体的温度每升高1℃,其内能增加74.8J,求电阻丝对气体提供的热量为多少?