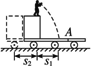
题目内容
平板车停在水平光滑的轨道上,平板车上有一人从固定在车上的货厢边沿水平方向顺着轨道方向跳出,落在平板车地板上的A点,距货厢水平距离为l=4 m,如图所示.人的质量为m,车连同货厢的质量为M=4 m,货厢高度为h=1.25 m,求:
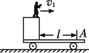
(1)车在人跳出后到落到地板期间的反冲速度;
(2)人落在车板上并站定以后,车还运动吗?车在地面上移动的位移是多少?
答案:
解析:
提示:
解析:
|
解析:人从货厢边跳离的过程,系统(人、车和货厢)的动量守恒;人落到车上的过程中,水平方向系统动量守恒,人在空中运动过程中做平抛运动,而车做匀速直线运动. 人从货厢边跳离的过程,系统(人、车和货厢)的动量守恒,设人的水平速度是v1.车的反冲速度是v2,则mv1-Mv2=0,v2= 人跳离货厢后做平抛运动,车以v2做匀速运动,运动时间为t=
s1+s2=l,即v1t+v2t=l 则v2= 车的水平位移为s2=v2t=1.6×0.5 m=0.8 m. 人落到车上A点的过程,系统水平方向的动量守恒(水平方向系统没受外力,而竖直方向支持力大于重力,合力不为零),人落到车上前的水平速度仍为v1,车的速度为v2,落到车上后设它们的共同速度为v,根据水平方向动量守恒得 mv1-Mv2=(M+m)v,则v=0. 故人落到车上A点站定后车的速度为零. |
提示:
|
对这种过程复杂的问题,要把它分解成几段简单过程,然后按每段过程所遵循的规律分别列方程求解. |

练习册系列答案
相关题目