Question

如图所示，有沿斜向固定的足够长的绝缘管道ab，其倾角为q ．管道内有一个质量为m带负电的小圆柱体P，所带电量的绝对值为q．P的横截面直径略小于管道的内径，它与管壁之间的动摩擦因数为m ．整个装置处于磁感应强度为B的匀强磁场中，磁场方向垂直管道而远离读者(即垂直纸面向里)．小圆柱体P从管道内的顶部由静止释放后将沿管道下滑，试求P下滑的最大速度(设P所带电量保持不变)．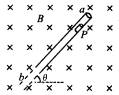

Answer 1

答案：见详解
解析：

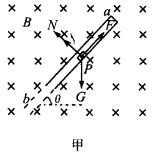
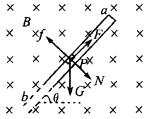
本题常见解答为：依题意，带电小圆柱体P释放后将沿管道加速下滑，且受到四个外力，即重力G=mg，管道壁对它的支持力N和滑动摩擦力F=mN，还有洛伦兹力f(其方向由左手定则判断)，如图甲所示．当P下滑至做匀速运动时达最大速度，设该速度为vm，相应的洛伦兹力f=qvmB．依据平衡条件可得 　　平行斜管方向　mgsinq -mN=0　　　　　　　　　　　　　　　　　　　　　　　① 　　垂直斜管方向　N+qvmB-mgcosq =0　　　　　　　　　　　　　　　　　　　　 ② 　　联解①、②两式可得 vm= 　　先分析带电小圆柱体P沿管道下滑的物理过程的变化情形，大致可分为三个阶段：第一阶段P做的是加速度逐渐增大的变加速运动，其受力情形如图甲所示．P被释放而沿管道下滑时，因其速度的增大，它所受的洛伦兹力(垂直管道向上)随之增大，那么管道下壁(相当于斜面)对它的支持力和相应的摩擦力将逐渐减小直至减为零，显然，在这一阶段中P沿管道下滑的加速度和速度均将逐渐增大．第二阶段P做的是加速度逐渐减小直至为零的变加速运动．当下管壁对P的支持力减至零时，在洛伦兹力的作用下．随即P将贴着上管壁向下滑动，其受力情形如图乙所示．此后上管壁对P的压力(垂直上管壁向下)和摩擦力均将随洛伦兹力的增大而变大，其加速度将逐渐减小直至趋于零(可近似为零)，而其速度却仍在增大直至最大．第三阶段P做的是匀速直线运动，其受力情形仍如图乙所示．当P下滑的加速度减为零时，可以认为它将以其最大速度贴着上管壁下滑做匀速直线运动．  乙 　　可见，本题的常见解答只考虑了带电小圆柱体P在上述物理过程第一阶段的受力情形，且滥用平衡条件列方程．如果磁场方向恰与题设方向相反，相应于P所受的洛伦兹力电该反向即变为垂直管壁向下，那么它开始就将做加速度逐渐减小而速度逐渐增大直至最大的变加速运动，此时上述解答才是对的．对这一物理过程比较简单的情形，学生是较为熟知的，而有的学生却因思维的惰性，不能随机应变，忽略本例物理过程的变化，从而导致失误． 　　正确解答如下：依上述分析可知，要求出带电小圆柱体P沿斜管下滑的最大速度(设为vm)，应选择上述物理过程中的第三个阶段(其受力情形如图乙所示)，且依平衡条件列出方程： 　　平行斜管方向　mgsinq -mN=0　　　　　　　　　　　　　　　　　　　　　　　③ 　　垂直斜管方向　qvmB-mgcosq -N=0　　　　　　　　　　　　　　　　　　　　　④ 　　联解③、④两式可得 vm=

提示：