题目内容
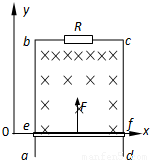
如图所示,足够长的光滑导轨ab、cd 固定在竖直平面内,导轨间距为l,b、c两点间接一阻值为R的电阻.ef是一水平放置的导体杆,其质量为m、电阻值为2R,杆与ab、cd 保持良好接触.整个装置放在磁感应强度满足B=B+ky的非匀强磁场中,磁场方向与导轨平面垂直.现用一竖直向上的力拉导体杆,使导体杆由y=0从静止开始做加速度为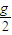 的匀加速运动,在金属杆ef上升了h高度的过程中,bc间电阻R产生的焦耳热为Q.重力加速度为g,不计导轨电阻及感应电流间的相互作用.求:
的匀加速运动,在金属杆ef上升了h高度的过程中,bc间电阻R产生的焦耳热为Q.重力加速度为g,不计导轨电阻及感应电流间的相互作用.求:(1)导体杆上升高度h过程中拉力做的功;
(2)导体杆上升到h时所受拉力F的大小;
(3)导体杆上升到h过程中通过杆的电量.
【答案】分析:(1)由运动学公式求出ef导体杆上升高度h时的速度,由焦耳定律求出导体杆上产生的焦耳热.导体杆ef克服安培力做功等于整个电路中产生的焦耳定律,根据动能定理求解拉力做的功;
(2)导体杆上升到h时,由欧姆定律求出回路中的感应电流,由F=BIL求出此时导体杆所受的安培力,由牛顿第二定律求解所受拉力F的大小;
(3)由法拉第电磁定律和欧姆定律推导出感应电量q,得到q=q=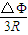 ,作出BL-y图象,图象的“面积”等于△Φ,即可求出电量.
,作出BL-y图象,图象的“面积”等于△Φ,即可求出电量.
解答:解:(1)设ef导体杆上升高度h,速度为v1,由运动学公式得:v1=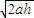 =
=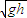 .
.
bc间电阻R产生的焦耳热为Q,导体杆的电阻值为2R,则金属杆上产生的焦耳热为2Q,根据功能关系可知,导体杆ef克服安培力做功为W安=3Q.
由动能定理得 WF-mgh-W安=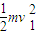
解得,WF= +3Q.
+3Q.
(2)设导体杆上升到h时拉力为F,根据闭合电路欧姆定律得
I1= =
=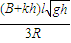
杆所受的安培力为 FA=ByI1l=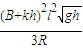
根据牛顿第二定律得
F-mg-FA=ma
综合各式得 F=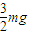 +
+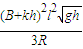 .
.
(3)由闭合电路欧姆定律得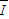 =
=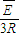
由法拉第电磁感应定律得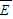 =
=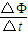
通过杆的电量 q=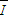 ?△t=
?△t=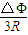
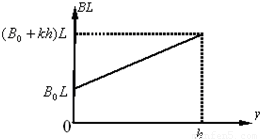
因为B与y成线性关系,可画出BL-y图象如图所示,可求得△Φ= [BL+(B+kh)L)h]
[BL+(B+kh)L)h]
则解得,q=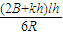
答:
(1)导体杆上升高度h过程中拉力做的功为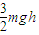 +3Q.;
+3Q.;
(2)导体杆上升到h时所受拉力F的大小为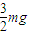 +
+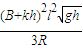 .;
.;
(3)导体杆上升到h过程中通过杆的电量为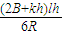 .
.
点评:本题综合性很强,一是推导安培力的表达式,二推导通过导体杆的电量,作出BL-y图象,由几何知识求出电量是本题的关键.
(2)导体杆上升到h时,由欧姆定律求出回路中的感应电流,由F=BIL求出此时导体杆所受的安培力,由牛顿第二定律求解所受拉力F的大小;
(3)由法拉第电磁定律和欧姆定律推导出感应电量q,得到q=q=
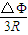 ,作出BL-y图象,图象的“面积”等于△Φ,即可求出电量.
,作出BL-y图象,图象的“面积”等于△Φ,即可求出电量.解答:解:(1)设ef导体杆上升高度h,速度为v1,由运动学公式得:v1=
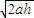 =
=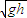 .
.
bc间电阻R产生的焦耳热为Q,导体杆的电阻值为2R,则金属杆上产生的焦耳热为2Q,根据功能关系可知,导体杆ef克服安培力做功为W安=3Q.
由动能定理得 WF-mgh-W安=
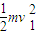
解得,WF=
 +3Q.
+3Q.(2)设导体杆上升到h时拉力为F,根据闭合电路欧姆定律得
I1=
 =
=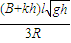
杆所受的安培力为 FA=ByI1l=
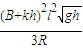
根据牛顿第二定律得
F-mg-FA=ma
综合各式得 F=
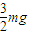 +
+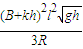 .
.(3)由闭合电路欧姆定律得
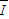 =
=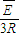
由法拉第电磁感应定律得
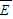 =
=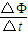
通过杆的电量 q=
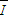 ?△t=
?△t=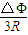
因为B与y成线性关系,可画出BL-y图象如图所示,可求得△Φ=
 [BL+(B+kh)L)h]
[BL+(B+kh)L)h]则解得,q=
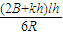
答:
(1)导体杆上升高度h过程中拉力做的功为
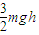 +3Q.;
+3Q.;(2)导体杆上升到h时所受拉力F的大小为
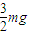 +
+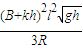 .;
.;(3)导体杆上升到h过程中通过杆的电量为
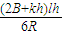 .
.点评:本题综合性很强,一是推导安培力的表达式,二推导通过导体杆的电量,作出BL-y图象,由几何知识求出电量是本题的关键.

练习册系列答案
相关题目
 如图所示,在MN的下方足够大的空间是玻璃介质,其折射率为n=
如图所示,在MN的下方足够大的空间是玻璃介质,其折射率为n= (2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( )
(2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( ) (1)下列说法正确的是
(1)下列说法正确的是
