题目内容
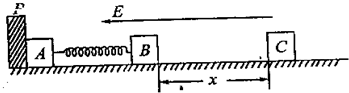
 如图,一“?”形绝缘导轨竖直放置,处在水平向右的匀强电场中.左边的半圆弧与水平杆ab、cd相切于a、c两点,两水平杆的高度差为h,杆长为4L,O为ad、bc连线的交点,虚线MN、M′N′的位置如图,其中aM=MM′=CN=NN′=L,M′b=N′d=2L.一质量为m,带电量为-q的小球穿在杆上.虚线MN左边的导轨光滑,虚线MN右边的导轨与小球之间的动摩擦因数为μ.已知:在O处没有固定点电荷+Q的时候,将带电小球自N点由静止释放后,小球刚好可到达a点.现在O处固定点电荷+Q,并将带电小球自d点以初速度v0向左瞬间推出.结果小球可沿杆运动到b点.(静电力恒量为k,重力加速度为g,在运动过程中+Q对-q的电场力始终小于小球的重力)求:
如图,一“?”形绝缘导轨竖直放置,处在水平向右的匀强电场中.左边的半圆弧与水平杆ab、cd相切于a、c两点,两水平杆的高度差为h,杆长为4L,O为ad、bc连线的交点,虚线MN、M′N′的位置如图,其中aM=MM′=CN=NN′=L,M′b=N′d=2L.一质量为m,带电量为-q的小球穿在杆上.虚线MN左边的导轨光滑,虚线MN右边的导轨与小球之间的动摩擦因数为μ.已知:在O处没有固定点电荷+Q的时候,将带电小球自N点由静止释放后,小球刚好可到达a点.现在O处固定点电荷+Q,并将带电小球自d点以初速度v0向左瞬间推出.结果小球可沿杆运动到b点.(静电力恒量为k,重力加速度为g,在运动过程中+Q对-q的电场力始终小于小球的重力)求:(1)匀强电场的电场强度E;
(2)运动过程中小球所受摩擦力的最大值fm和小球经过M′点时的加速度大小a;
(3)使小球能够运动到b点的初速度v0的最小值.
分析:(1)根据动能定理研究带电小球自N点由静止释放后,小球刚好可到达a点过程求出电场强度E
(2)运动过程中小球受重力、向上的弹力、向左的摩擦力、向左的电场力,指向O点的库仑力,根据正交分解可知:小球经过M′点时,球与轨道之间的弹力最大,所受的滑动摩擦力最大,再进行求解.
求出小球合力根据牛顿第二定律求解加速度.
(3)根据动能定理研究带电小球从d点到b点的过程求出初速度v0的最小值.
(2)运动过程中小球受重力、向上的弹力、向左的摩擦力、向左的电场力,指向O点的库仑力,根据正交分解可知:小球经过M′点时,球与轨道之间的弹力最大,所受的滑动摩擦力最大,再进行求解.
求出小球合力根据牛顿第二定律求解加速度.
(3)根据动能定理研究带电小球从d点到b点的过程求出初速度v0的最小值.
解答:解:(1)根据动能定理研究带电小球自N点由静止释放后,小球刚好可到达a点过程
由题意有:qEL-mgh=0-0=0
∴E=
(2)运动过程中小球受重力、向上的弹力、向左的摩擦力、向左的电场力,指向O点的库仑力,
根据正交分解可知:小球经过M′点时库仑力竖直向下达到最大值,球与轨道之间的弹力最大,所受的滑动摩擦力最大.
fm=μN=μ(mg+
)=μ(mg+
)
小球经过M′点时的加速度大小为:a=
=
=
+μ(g+
)
(3)根据对称性可知,由d→b,小球克服摩擦力做的功等效为:
Wf=mgμ×6L=6mgμL
而电场力做的功为零
∴初速度v0的最小值应满足:
m
=mgh+Wf
∴v0=
答:(1)匀强电场的电场强度是
;
(2)运动过程中小球所受摩擦力的最大值是μ(mg+
),小球经过M′点时的加速度大小是
+μ(g+
);
(3)使小球能够运动到b点的初速度v0的最小值是
.
由题意有:qEL-mgh=0-0=0
∴E=
| mgh |
| qL |
(2)运动过程中小球受重力、向上的弹力、向左的摩擦力、向左的电场力,指向O点的库仑力,
根据正交分解可知:小球经过M′点时库仑力竖直向下达到最大值,球与轨道之间的弹力最大,所受的滑动摩擦力最大.
fm=μN=μ(mg+
| kQq | ||
(
|
| 4kQq |
| (h)2 |
小球经过M′点时的加速度大小为:a=
| qE+fm |
| m |
| ||||
| m |
| gh |
| L |
| 4kQq |
| mh2 |
(3)根据对称性可知,由d→b,小球克服摩擦力做的功等效为:
Wf=mgμ×6L=6mgμL
而电场力做的功为零
∴初速度v0的最小值应满足:
| 1 |
| 2 |
| v | 2 0 |
∴v0=
| 2gh+12gμL |
答:(1)匀强电场的电场强度是
| mgh |
| qL |
(2)运动过程中小球所受摩擦力的最大值是μ(mg+
| 4kQq |
| (h)2 |
| gh |
| L |
| 4kQq |
| mh2 |
(3)使小球能够运动到b点的初速度v0的最小值是
| 2gh+12gμL |
点评:能够分析物体的受力情况和运动情况,选择合适的运动过程运用动能定理求解.
动能定理的优点在于适用任何运动包括曲线运动.动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.
动能定理的优点在于适用任何运动包括曲线运动.动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

练习册系列答案
相关题目