��Ŀ����
����Ŀ����ͼ��ij�Զ�����װ�õ����ͼ���������������ڵ���Сƽ̨����һ���ij��پ���λ����ֱ���ڵ������ķ�֮һԲ���νӶ��ɵĹ��������ߵ�P�ɳ�������ȹ��ڣ����������˶�ʹ��������ȣ�����������Ϊm��С������汻�������壬������װ�����о�һЩ�������⣮���С�����ķ�֮һԲ���İ뾶�ֱ�Ϊ2R��R��Сƽ̨��Բ�����⻬�����������ݽ��濴��������б��AB��CD��һ�ι⻬Բ��BC��ɣ�������б���Ķ�Ħ������Ϊ0.25���Ҳ����¶ȱ仯����б����Ǿ�Ϊ��=37�㣬AB=CD=2R��A��D�ȸߣ�D�˹̶�һС���壬����λ��Բ���ι�����ڵ���ֱƽ���ڣ���ײ����ʧ��е�ܣ�����ʼ����ͬһ����ֱƽ�����˶����������ٶ�Ϊg��
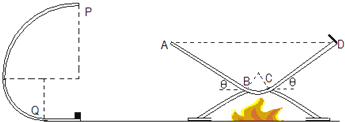
��1���������ǡ���ܾ�P��ɳ���Ϊ��ʹ����ǡ����ABб�������ڣ�Ӧ���ڹ���֧�ܸ߶�ʹб���A��D����ظ�Ϊ���٣�
��2���ӣ�1���ʣ����ڹ���б����ͨ������·�̣�
��3���Ի���IJ�ͬ���ٶȣ�����ͨ����ߵ�P��СԲ����͵�Qʱ��ѹ��֮�����Сֵ��
���𰸡���1��![]() ����2��
����2��![]() R����3��9mg��
R����3��9mg��
�������������������1����P��![]() �����
�����![]() ��
��
����A��ʱ�ٶȷ���Ҫ����AB��![]()
����AD��ظ߶�Ϊ��![]()
��2������A�㻬����ٶ�Ϊ��![]()
���辭��һ�������ܹ��ص�A�㣬�����ʱ����ΪEk��![]() ��
��
���Ի��鲻�Ử��A���ɳ���
���ݶ��ܶ����ã�![]()
�������ݽ�ã�1��2mgR��0��2mgs=![]()
��û����ڹ���б�����߹�����·�̣�![]()
��3������ٶȡ���ߵ��ٶȷֱ�Ϊv1��v2��
��ţ�����ɣ���Q�㣬![]() �����
�����![]()
��P�㣬![]() �����
�����![]()
���ԣ�![]()
�ɻ�е���غ�ã�![]()
��![]() Ϊ��ֵ��
Ϊ��ֵ��
����v2����Сֵ![]() ����ѹ�������СֵΪ9mg��
����ѹ�������СֵΪ9mg��