��Ŀ����
5�������Ϻ�����ߡ���·��������·ȫ��ͨ���������·��װ��һ�ֵ��װ�ÿ�����������Ĵ����źţ���ȷ����λ�ú��˶�״̬����ԭ���ǽ��ܲ�����ǿ�ų��Ĵ�����װ�ڻ��ڳ������棬��ͼ����ʾ������ͼ����������������������������Ȧʱ����Ȧ�����һ�����źŴ�����������ģ���Ȧ�߳��ֱ�Ϊl1��l2������Ϊn����Ȧ�ʹ����ߵĵ�����Բ��ƣ�����ͨ����Ȧʱ���������Ľ��յ���Ȧ���˵ĵ�ѹ�ź�u��ʱ��t�Ĺ�ϵ��ͼ����ʾ��ab��cd��Ϊֱ�ߣ���t1��t2��t3��t4���˶����̵��ĸ�ʱ�̣����������
| A�� | ��t1��t2ʱ�������ȼ���ֱ���˶� | |
| B�� | ��t3��t4ʱ�������ȼ���ֱ���˶� | |
| C�� | ��t1��t2ʱ���ڼ��ٶȴ�СΪ$\frac{{{u_2}-{u_1}}}{{nB{l_1}��{t_2}-{t_1}��}}$ | |
| D�� | ��t3��t4ʱ����ƽ���ٶȵĴ�СΪ$\frac{{{u_3}+{u_4}}}{{2nB{l_1}}}$ |
���� Ҫ�ж����˶�״̬�������ҳ���Ӧ�綯�����ٶȵĹ�ϵ������ȷ���ٶȺ�ʱ��Ĺ�ϵ���Ϳ���֪�����˶����ʣ����ٶȿ�����A��B�������ж������ٶ�ʱ���ϵ��ȷ�������ݻ��˶����������ٶ�ʱ���ϵ�����ƽ���ٶȣ�
��� �⣺
A����E=BLv��֪����Ӧ�綯�����ٶȳ����ȣ�����ab�εĵ�ѹ��ʱ�����������˿�֪��t1��t2���ʱ���ڣ����ٶ���ʱ��Ҳ�����������Ի������ʱ�����������ȼ���ֱ���˶�����A��ȷ��
B��ͬ������t3��t4ʱ�������ȼ���ֱ���˶�����B����
C����ͼ֪t1ʱ�̶�Ӧ���ٶ�Ϊ v1=$\frac{{u}_{1}}{nB{l}_{1}}$��t2ʱ�̶�Ӧ���ٶ�Ϊv2=$\frac{{u}_{2}}{nB{l}_{1}}$�������ʱ���ڵļ��ٶ�Ϊ��a=$\frac{{v}_{2}-{v}_{1}}{{t}_{2}-{t}_{1}}$=$\frac{{{u_2}-{u_1}}}{{nB{l_1}��{t_2}-{t_1}��}}$����C��ȷ��
D����ͼ֪t3ʱ�̶�Ӧ���ٶ�Ϊ v3=$\frac{{u}_{3}}{nB{l}_{1}}$��t4ʱ�̶�Ӧ���ٶ�Ϊv4=$\frac{{u}_{4}}{nB{l}_{1}}$�������ʱ���ڵ�ƽ���ٶ�Ϊ$\overline{v}$=$\frac{{v}_{3}+{v}_{4}}{2}$=$\frac{{{u_3}+{u_4}}}{{2nB{l_1}}}$����D��ȷ��
��ѡ��ACD��
���� ����ؼ������ж������˶����ʣ������ǿ�����ͼ��ʱ���ѹ�Ǻ��ٶȳ����ȵģ���Ӧ��ϵ�йض����綯�ƵĹ�ʽ���Խ����ٶ���ʱ��Ĺ�ϵ���������Եó���ȷ���ۣ���������˼ά��ѵ����

 ij�糡�ĵ糡�߷ֲ���ͼ��ʾ���ڵ糡������a��b��c���㣬��a��b������b��c��࣬������
ij�糡�ĵ糡�߷ֲ���ͼ��ʾ���ڵ糡������a��b��c���㣬��a��b������b��c��࣬������| A�� | a�㳡ǿ����b�㳡ǿ | |
| B�� | a����Ƹ���b����� | |
| C�� | ������c��ĵ�����С����a��ĵ����� | |
| D�� | a��b�����ĵ��Ʋ�С��b��c�����ĵ��Ʋ� |
 ��ͼ��ʾ�������ֱ�Ϊm1��m2������������������ϸ�ߣ��ֱ��������컨���ϵ�A��B���㣬������ˮƽ����нǷֱ�Ϊ�������Ҧ����£������������ʵ���ǡ�ô���ˮƽ״̬���������������ֱ�ΪTA��TB��������˵������ȷ���ǣ�������
��ͼ��ʾ�������ֱ�Ϊm1��m2������������������ϸ�ߣ��ֱ��������컨���ϵ�A��B���㣬������ˮƽ����нǷֱ�Ϊ�������Ҧ����£������������ʵ���ǡ�ô���ˮƽ״̬���������������ֱ�ΪTA��TB��������˵������ȷ���ǣ�������| A�� | TA��TB | B�� | TA��TB | C�� | m1��m2 | D�� | m1��m2 |
 ��ͼ��ʾ������ֱ��������OCD�ɲ�ͬ����A��Bƴ�Ӷ��ɣ�PΪ��������CD���ϵĽ��㣬��DP��CP����OD��ˮƽ���ã���С���Ӿ�ֹ��C����D��Ȼ��OC��ˮƽ���ã����� С���Ӿ�ֹ��D����C��С������δӶ��㻬��P���ʱ����ͬ���һ����������������� ��������־�ֹ��������˵������ȷ���ǣ�������
��ͼ��ʾ������ֱ��������OCD�ɲ�ͬ����A��Bƴ�Ӷ��ɣ�PΪ��������CD���ϵĽ��㣬��DP��CP����OD��ˮƽ���ã���С���Ӿ�ֹ��C����D��Ȼ��OC��ˮƽ���ã����� С���Ӿ�ֹ��D����C��С������δӶ��㻬��P���ʱ����ͬ���һ����������������� ��������־�ֹ��������˵������ȷ���ǣ�������| A�� | A��B�����ϵĶ�Ħ��������ͬ | |
| B�� | ���λ�������鵽��P��������� | |
| C�� | ���λ�������鵽���������� | |
| D�� | ���λ�������鵽���Ħ�����Ȳ���� |

| A�� | �����������ΪQ������ɾ���Ϊxʱ�����������Ϊ$\frac{kqQ}{x}$ | |
| B�� | �����������ٵط��ھ��볡Դ����x1�����������ͣ�ھ��볡Դ����$\frac{kqQ}{?mg{x}_{1}}$�� | |
| C�� | �����������ٵط��ھ��볡Դ����x1�����������˶������볡Դ����x3���ļ��ٶ�Ϊ$\frac{kqQ}{m{x}_{1}{x}_{3}-��g}$ | |
| D�� | �����������ٵط��ھ��볡Դ����x1�����������˶������볡Դ����x3�����ٶ�ΪV=$\sqrt{��\frac{2qkQ}{m{x}_{1}{x}_{3}}-2��g����{x}_{3}-{x}_{1}��}$ |
 ��ͼ��ʾ���ռ����߿�������ǿ�糡��AA�䣬BB�䣬CC���Ǹõ糡�����������棬���ڵ������ľ���Ϊ1cm������BB��Ϊ��������森һ����Ϊm�����翗Ϊ+q��������AA'�����Գ��ٶ�v0��ͼ�е�P�����糡���պô�C����뿪�糡����֪PA��=2cm���ӵ��������Բ��ƣ���˵������ȷ���ǣ�������
��ͼ��ʾ���ռ����߿�������ǿ�糡��AA�䣬BB�䣬CC���Ǹõ糡�����������棬���ڵ������ľ���Ϊ1cm������BB��Ϊ��������森һ����Ϊm�����翗Ϊ+q��������AA'�����Գ��ٶ�v0��ͼ�е�P�����糡���պô�C����뿪�糡����֪PA��=2cm���ӵ��������Բ��ƣ���˵������ȷ���ǣ�������| A�� | ��������P��ʱ�ĵ�������2mv02 | |
| B�� | �����ӵ���C���ʱ���ٶ���$\sqrt{2}$v0 | |
| C�� | �����ӵ���C���ʱ�ĵ�������mv02 | |
| D�� | ������ͨ��������BB��ʱ�Ķ�����1.5mv02 |
 ��ͼ����ʾ���⻬ƽ�н�������MN��PQ����ƽ����ˮƽ��ɦȽǣ�M��P���˽�һ����R������װ�ô��ڷ���ֱ����ƽ�����ϵ���ǿ�ų��У�t=0ʱ�Խ�����ʩ��һƽ���ڵ��������F��ʹ�������ɾ�ֹ��ʼ�ص��������˶�������������Ϊr�����������Բ��ƣ���֪ͨ������R�ĸ�Ӧ����I��ʱ��t�仯�Ĺ�ϵ��ͼ����ʾ�����й��ڰ��˶��ٶ�v������F������R�ĵ���q�Լ��պϻ�·�д�ͨ���ı仯��$\frac{����}{��t}$��ʱ��仯��ͼ����ȷ���ǣ�������
��ͼ����ʾ���⻬ƽ�н�������MN��PQ����ƽ����ˮƽ��ɦȽǣ�M��P���˽�һ����R������װ�ô��ڷ���ֱ����ƽ�����ϵ���ǿ�ų��У�t=0ʱ�Խ�����ʩ��һƽ���ڵ��������F��ʹ�������ɾ�ֹ��ʼ�ص��������˶�������������Ϊr�����������Բ��ƣ���֪ͨ������R�ĸ�Ӧ����I��ʱ��t�仯�Ĺ�ϵ��ͼ����ʾ�����й��ڰ��˶��ٶ�v������F������R�ĵ���q�Լ��պϻ�·�д�ͨ���ı仯��$\frac{����}{��t}$��ʱ��仯��ͼ����ȷ���ǣ�������




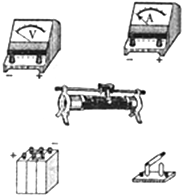 ij��ѹ����������20-30k��֮�䣬Ϊ�˲��������裬ʵ�����ṩ�����п��õ����ģ�
ij��ѹ����������20-30k��֮�䣬Ϊ�˲��������裬ʵ�����ṩ�����п��õ����ģ�