题目内容
制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示,加在极板A、B间的电压UAB作周期性变化,其正向电压为U0,反向电压为-kU0(k>1),
电压变化的周期为2r,如图乙所示。在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动。若整个运动过程中,电子未碰到极板A,且不考虑重力作用。
(1)若 ,电子在0—2r时间内不能到达极板A,求d应满足的条件;
,电子在0—2r时间内不能到达极板A,求d应满足的条件;
(2)若电子在0—2r时间未碰到极板B,求此运动过程中电子速度 随时间t变化的关系;
随时间t变化的关系;
(3)若电子在第N个周期内的位移为零,求k的值。

(1)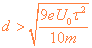
(2)v=[t-(k+1)n ]
]
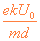 ,(n=0,1,2, ……,99)和v=[(n+1)(k+1)
,(n=0,1,2, ……,99)和v=[(n+1)(k+1) -kt]
-kt]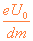 ,(n=0,1,2, ……,99)
,(n=0,1,2, ……,99)
(3)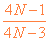
【解析】(1)电子在 0~τ时间内做匀加速运动
加速度的大小 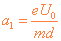 ①
①
位移
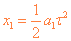 ②
②
在τ~2τ时间内先做匀减速运动,后反向做匀加速运动
加速度的大小 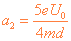 ③
③
初速度的大小 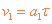 ④
④
匀减速运动阶段的位移 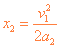 ⑤
⑤
依据题,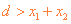 解得
解得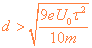 ⑥
⑥
(2)在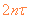 ~
~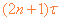 ,(n=0,1,2,……99)时间内
,(n=0,1,2,……99)时间内
速度增量 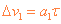 ⑦
⑦
在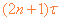 ~
~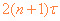 ,(n=0,1,2,……99)时间内
,(n=0,1,2,……99)时间内
加速度的大小 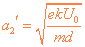
速度增量 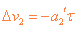 ⑧
⑧
(a)当0≤ ~
~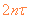 <
< 时
时
电子的运动速度 v=n△v1+n△v2+a1(t-2n ) ⑨
) ⑨
解得 v=[t-(k+1)n ]
] 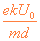 ,(n=0,1,2, ……,99) ⑩
,(n=0,1,2, ……,99) ⑩
(b)当0≤t-(2n+1) <
< 时
时
电子的运动速度 v=(n+1)
△v1+n△v2-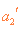 [t-(2n+1)
[t-(2n+1) ] ⑾
] ⑾
解得v=[(n+1)(k+1) -kt]
-kt]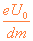 ,(n=0,1,2, ……,99) ⑿
,(n=0,1,2, ……,99) ⑿
(3)电子在2(N-1) ~(2N-1)
~(2N-1) 时间内的位移x2N-1=v2N-2
时间内的位移x2N-1=v2N-2 +
+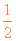 a1
a1 2
2
电子在(2N-1) ~2NT时间内的位移x2N=v2N-1
~2NT时间内的位移x2N=v2N-1 -
-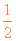
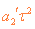
由⑩式可知 v2N-2=(N-1)(1-k)
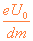
由⑿式可知 v2N-1=(N-Nk+k)
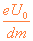
依题意得 x2N-1+x2N=0
解得: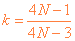

 制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示.加在极板A、B间的电压UAB按图乙所示规律变化:在0-T0时间内电压为U0,此后电压呈周期性变化,电压大小为kU0,电压变化的周期为2τ.在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动.若无论经过多长的时间,这个电子既未碰到极板A,也没有碰到极板B,且不考虑重力作用.
制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示.加在极板A、B间的电压UAB按图乙所示规律变化:在0-T0时间内电压为U0,此后电压呈周期性变化,电压大小为kU0,电压变化的周期为2τ.在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动.若无论经过多长的时间,这个电子既未碰到极板A,也没有碰到极板B,且不考虑重力作用.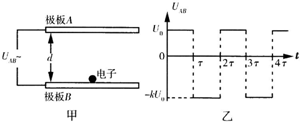 制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示,加在极板A、B间的电压UAB作周期性变化,其正向电压为U0,反向电压为-kU0(k>1),电压变化的周期为2r,如图乙所示.在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动.若整个运动过程中,电子未碰到极板A,且不考虑重力作用.
制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示,加在极板A、B间的电压UAB作周期性变化,其正向电压为U0,反向电压为-kU0(k>1),电压变化的周期为2r,如图乙所示.在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动.若整个运动过程中,电子未碰到极板A,且不考虑重力作用.
