题目内容
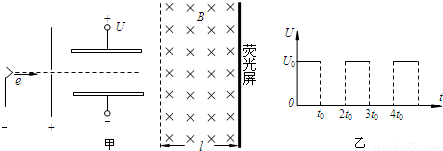
如图所示装置由加速电场、偏转电场和偏转磁场组成.偏转电场处在加有电压的相距为d的两块水平平行放置的导体板之间,匀强磁场水平宽度为l,竖直宽度足够大,处在偏转电场的右边,如图甲所示.大量电子(其重力不计)由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间射入偏转电场.当两板没有加电压时,这些电子通过两板之间的时间为2t,当在两板间加上如图乙所示的周期为2t、幅值恒为U的电压时,所有电子均能通过电场,穿过磁场,最后打在竖直放置的荧光屏上(已知电子的质量为m、电荷量为e).求:(1)如果电子在t=0时刻进入偏转电场,求它离开偏转电场时的侧向位移大小;
(2)通过计算说明,所有通过偏转电场的电子的偏向角(电子离开偏转电场的速度方向与进入电场速度方向的夹角)都相同.
(3)要使电子能垂直打在荧光屏上,匀强磁场的磁感应强度为多少?
【答案】分析:电子垂直进入匀强电场时可能先做类平抛运动后再做匀速直线运动,也可能先做匀速直线运动后再做类平抛;当垂直进入匀强磁场时做匀速圆周运动.当电子从零时刻开始进入则先做类平抛运动后匀速直线运动.在电场中的偏向角由沿电场方向的速度与垂直电场方向的速度的正切值来确定.若电子垂直打在荧光屏上,则由几何关系可确定运动轨迹的半径与已知长度的关系,从而算出磁感应强度.
解答: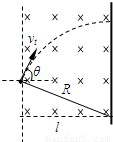 解:(1)在t=0时刻,电子进入偏转电场,
解:(1)在t=0时刻,电子进入偏转电场,
Ox方向(水平向右为正)做匀速直线运动.
Oy方向(竖直向上为正)在0-t时间内受电场力作用做匀加速运动,
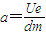
在t-2t时间内做匀速直线运动,
速度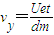
侧向位移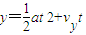
得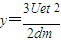
(2)设电子以初速度v=vx进入偏转电场,在偏转电场中受电场力作用而加速.
不管电子是何时进入偏转电场,在它穿过电场的2t时间内,
其Oy方向的加速度或者是
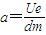 (电压为U时),
(电压为U时),
或者是0(电压为0时).
△v=a△t,它在Oy方向上速度增加量都为
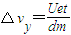 .
.
因此所有电子离开偏转电场时的Oy方向的分速度都相等为
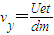 ;
;
Ox方向的分速度都为v=vx,
所有电子离开偏转电场的偏向角都相同.
(3)设电子从偏转电场中射出时的偏向角为θ,
电子进入匀强磁场后做圆周运动垂直打在荧光屏上,
如图所示.电子在磁场中运动的半径:
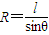
设电子从偏转电场中出来时的速度为vt,
则电子从偏转电场中射出时的偏向角为:
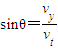
电子进入磁场后做圆周运动,
其半径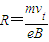
由上述四式可得:
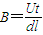 .
.
点评:带电粒子在垂直的电场中做类平抛运动,在垂直的磁场中做匀速圆周运动.类平抛运动可用平抛运动规律来处理,圆周运动的可建立几何关系来列式求解.
解答:
 解:(1)在t=0时刻,电子进入偏转电场,
解:(1)在t=0时刻,电子进入偏转电场,Ox方向(水平向右为正)做匀速直线运动.
Oy方向(竖直向上为正)在0-t时间内受电场力作用做匀加速运动,
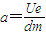
在t-2t时间内做匀速直线运动,
速度
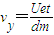
侧向位移
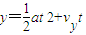
得
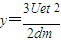
(2)设电子以初速度v=vx进入偏转电场,在偏转电场中受电场力作用而加速.
不管电子是何时进入偏转电场,在它穿过电场的2t时间内,
其Oy方向的加速度或者是
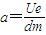 (电压为U时),
(电压为U时),或者是0(电压为0时).
△v=a△t,它在Oy方向上速度增加量都为
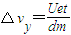 .
.因此所有电子离开偏转电场时的Oy方向的分速度都相等为
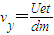 ;
;Ox方向的分速度都为v=vx,
所有电子离开偏转电场的偏向角都相同.
(3)设电子从偏转电场中射出时的偏向角为θ,
电子进入匀强磁场后做圆周运动垂直打在荧光屏上,
如图所示.电子在磁场中运动的半径:
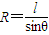
设电子从偏转电场中出来时的速度为vt,
则电子从偏转电场中射出时的偏向角为:
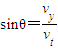
电子进入磁场后做圆周运动,
其半径
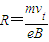
由上述四式可得:
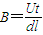 .
.点评:带电粒子在垂直的电场中做类平抛运动,在垂直的磁场中做匀速圆周运动.类平抛运动可用平抛运动规律来处理,圆周运动的可建立几何关系来列式求解.

练习册系列答案
相关题目
 (2011?海淀区模拟)如图所示装置可用来分析气体原子的组成.首先使待研究气体进入电离室A,在此气体被电离成等离子体(待研究气体的等离子体由含有一价正离子和电荷量为e的电子组成,整体显电性).这些等离子体(统称“带电粒子”)从电离室下端狭缝S1飘出(忽略飘出的速度),经两极板间电压为U的加速电场后(忽略这些带电粒子被加速的时间),从狭缝S2沿垂直磁场方向进入磁感应强度为B的有界匀强磁场,在磁场的上、下边界处分别装有水平底片E和F.当双刀双掷开关分别掷向1、2和3、4时,发现从电离室狭缝S1飘出的带电粒子分别打在E和F上的P、Q点.已知狭缝S2与水平底片E上P点之间的距离d1=2.0cm,到水平底片F上Q点的水平距离d2=6.4cm,磁场区域宽度d=30cm.空气阻力、带电粒子所受重力以及带电粒子之间的相互作用均可忽略不计.
(2011?海淀区模拟)如图所示装置可用来分析气体原子的组成.首先使待研究气体进入电离室A,在此气体被电离成等离子体(待研究气体的等离子体由含有一价正离子和电荷量为e的电子组成,整体显电性).这些等离子体(统称“带电粒子”)从电离室下端狭缝S1飘出(忽略飘出的速度),经两极板间电压为U的加速电场后(忽略这些带电粒子被加速的时间),从狭缝S2沿垂直磁场方向进入磁感应强度为B的有界匀强磁场,在磁场的上、下边界处分别装有水平底片E和F.当双刀双掷开关分别掷向1、2和3、4时,发现从电离室狭缝S1飘出的带电粒子分别打在E和F上的P、Q点.已知狭缝S2与水平底片E上P点之间的距离d1=2.0cm,到水平底片F上Q点的水平距离d2=6.4cm,磁场区域宽度d=30cm.空气阻力、带电粒子所受重力以及带电粒子之间的相互作用均可忽略不计.




