题目内容
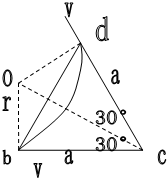
 (2006?广东模拟)如图所示,边长为a的等边三角形bcd所围区域内磁感应强度为B,方向垂直纸面向内的匀强磁场,某时刻静止在b点的原子核X发生α衰变,α粒子沿bc方向射入磁场,经磁场偏转后恰好在d点沿cd方向射出.已知α粒子质量为m,电量为2e,剩余核的质量为M,衰变过程的核能全部转化为动能,求原子核X的质量MX.
(2006?广东模拟)如图所示,边长为a的等边三角形bcd所围区域内磁感应强度为B,方向垂直纸面向内的匀强磁场,某时刻静止在b点的原子核X发生α衰变,α粒子沿bc方向射入磁场,经磁场偏转后恰好在d点沿cd方向射出.已知α粒子质量为m,电量为2e,剩余核的质量为M,衰变过程的核能全部转化为动能,求原子核X的质量MX.分析:由题意,原子核X发生了衰变,要求原子核X的质量MX,应根据爱因斯坦质能方程求衰变所释放的核能.而衰变过程的核能全部转化为动能,则必须求出α粒子和剩余核的动能.先画出α粒子的运动轨迹,由几何知识求出轨迹半径,即可由牛顿第二定律求出其速率,根据衰变过程动量守恒求得剩余核的速率,就可以求得衰变后总动能,即得到核能,再由爱因斯坦质能方程求MX.
解答:解:由题意画出α粒子在磁场中的运动轨迹如图所示,由几何关系,由由几何知识得:α粒子的运动半径为:
 R=atanθ=
R=atanθ=
a
在磁场中,对α粒子:
2eBv=m
∴v=
=
?
衰变过程中动量守恒:
mv-Mu=0
则得剩余核的速率 u=
=
?
衰变过程中释放的能量:△E=
mv2+
Mu2=
?
由爱因斯坦质能方程:△m=
=
?
原子核X的质量为:MX=m+M+△m=(m+M)(1+
)
答:原子核X的质量MX是(m+M)(1+
).
 R=atanθ=
R=atanθ=
| ||
| 3 |
在磁场中,对α粒子:
2eBv=m
| v2 |
| r |
∴v=
| 2eBr |
| m |
2
| ||
| 3 |
| eBa |
| m |
衰变过程中动量守恒:
mv-Mu=0
则得剩余核的速率 u=
| 2eBr |
| m |
2
| ||
| 3 |
| eBa |
| M |
衰变过程中释放的能量:△E=
| 1 |
| 2 |
| 1 |
| 2 |
| 2e2B2a2 |
| 3 |
| m+M |
| Mm |
由爱因斯坦质能方程:△m=
| △E |
| c2 |
| 2e2B2a2 |
| 3c2 |
| m+M |
| Mm |
原子核X的质量为:MX=m+M+△m=(m+M)(1+
| 2e2B2a2 |
| 3c2Mm |
答:原子核X的质量MX是(m+M)(1+
| 2e2B2a2 |
| 3c2Mm |
点评:本题是带电粒子在磁场中的圆周运动与原子核衰变的综合,要抓住衰变过程遵守动量守恒和能量守恒进行分析.磁场中要画出轨迹,运用几何知识和牛顿第二定律进行研究.

练习册系列答案
相关题目