题目内容
 (2013?厦门一模)如图所示,MN为两平行金属板,O、O为两金属板中心处正对的两个小孔,N板的右侧空间有磁感应强度大小均为B且方向相反的两匀强磁场区,图中N板与虚线CD、PQ为两磁场边界线,三条界线平行,两磁场区域的宽度分别为d和3d,沿边界线方向磁场区域足够大.在两金属板上加上大小可调节的直流电压,质量为m、电量为-q的带电粒子(重力不计);从O点由静止释放,经过MN板间的电场加速后,从O'沿垂直于磁场方向射入磁场,若粒子能穿过CD界并进入CD右侧磁场但不能穿过PQ界,最终打到N板而结束运动,试求:
(2013?厦门一模)如图所示,MN为两平行金属板,O、O为两金属板中心处正对的两个小孔,N板的右侧空间有磁感应强度大小均为B且方向相反的两匀强磁场区,图中N板与虚线CD、PQ为两磁场边界线,三条界线平行,两磁场区域的宽度分别为d和3d,沿边界线方向磁场区域足够大.在两金属板上加上大小可调节的直流电压,质量为m、电量为-q的带电粒子(重力不计);从O点由静止释放,经过MN板间的电场加速后,从O'沿垂直于磁场方向射入磁场,若粒子能穿过CD界并进入CD右侧磁场但不能穿过PQ界,最终打到N板而结束运动,试求:(1)粒子要能穿过CD界并进入CD右侧磁场,MN板间的电压至少要大于多少;
(2)粒子不穿过PQ界,粒子从O射入磁场所允许的最大速率;
(3)最大速率射入磁场的粒子在磁场中运动的总时间.
分析:先由动能定理求出加速场中加速后获得的速度的表达式;由几何关系确定半径然后由根据牛顿第二定律列方程;
先画出粒子在右边磁场的运动轨迹,相切时为临界情况,由几何关系确定半径,然后求得速度v;
确定出粒子偏转的圆心角,然后根据周期公式求运动时间.
先画出粒子在右边磁场的运动轨迹,相切时为临界情况,由几何关系确定半径,然后求得速度v;
确定出粒子偏转的圆心角,然后根据周期公式求运动时间.
解答:解:(1)设MN间电压为U0时,若粒子在CD左侧磁场中运动的圆弧与CD界相切,如图甲,
粒子经电场加速:qU0=
mv02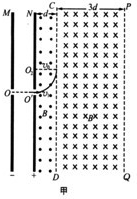
在磁场中运动的圆周半径:r0=d
qBv0=m
由上述得:U0=
粒子要穿过C界,电压应大于:
.
(2)设粒子射入磁场速度为v时,粒子在CD左侧轨迹圆心为O1,右侧轨迹圆心为O2且圆弧与PQ相切,恰好不射出PQ界,
如图乙,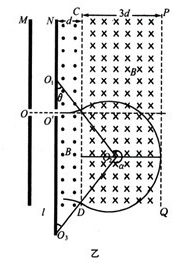
有:左右两圆周半径相同,均为r=2d
qBv=
得:v=
(3)由图得圆弧圆心角为θ=
,α=
粒子圆周运动周期:T=
=
粒子经过三段圆弧运动时间分别为:
t1=t3=
T
t2=
T
在磁场中运动总时间:t=t1+t2+t3=
答:(1)粒子要能穿过CD界并进入CD右侧磁场,MN板间的电压至少要大于:
;
(2)粒子不穿过PQ界,粒子从O射入磁场所允许的最大速率为
;
(3)最大速率射入磁场的粒子在磁场中运动的总时间为
.
粒子经电场加速:qU0=
| 1 |
| 2 |

在磁场中运动的圆周半径:r0=d
qBv0=m
| v02 |
| r0 |
由上述得:U0=
| qB2d2 |
| 2m |
粒子要穿过C界,电压应大于:
| qB2d2 |
| 2m |
(2)设粒子射入磁场速度为v时,粒子在CD左侧轨迹圆心为O1,右侧轨迹圆心为O2且圆弧与PQ相切,恰好不射出PQ界,
如图乙,

有:左右两圆周半径相同,均为r=2d
qBv=
| mv2 |
| r |
得:v=
| 2qBd |
| m |
(3)由图得圆弧圆心角为θ=
| π |
| 6 |
| 4π |
| 3 |
粒子圆周运动周期:T=
| 2πr |
| v |
| 2πm |
| qB |
粒子经过三段圆弧运动时间分别为:
t1=t3=
| θ |
| 2π |
t2=
| α |
| 2π |
在磁场中运动总时间:t=t1+t2+t3=
| 5πm |
| 3qB |
答:(1)粒子要能穿过CD界并进入CD右侧磁场,MN板间的电压至少要大于:
| qB2d2 |
| 2m |
(2)粒子不穿过PQ界,粒子从O射入磁场所允许的最大速率为
| 2qBd |
| m |
(3)最大速率射入磁场的粒子在磁场中运动的总时间为
| 5πm |
| 3qB |
点评:本题考查了带电粒子在磁场中的圆周运动,关键是能画出临界情况的运动轨迹.

练习册系列答案
相关题目
 (2013?厦门一模)如图所示,有一个人站在超市的自动电梯(斜面电梯)上,若人和电梯一起斜向下匀速运动,则电梯对此人的作用力为( )
(2013?厦门一模)如图所示,有一个人站在超市的自动电梯(斜面电梯)上,若人和电梯一起斜向下匀速运动,则电梯对此人的作用力为( )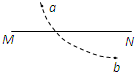 (2013?厦门一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子不计重力从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
(2013?厦门一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子不计重力从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( ) (2013?厦门一模)下列四幅图的有关说法中正确的是( )
(2013?厦门一模)下列四幅图的有关说法中正确的是( ) (2013?厦门一模)如图所示的远距离输电电路图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压及输电线的电阻均不变.在用电高峰期,随着发电厂输出功率的增大,下列说法正确的有( )
(2013?厦门一模)如图所示的远距离输电电路图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压及输电线的电阻均不变.在用电高峰期,随着发电厂输出功率的增大,下列说法正确的有( )