题目内容
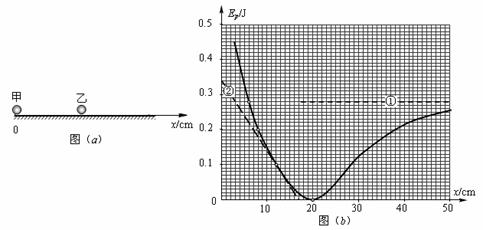
如图(a)所示,小球甲固定于足够长光滑水平面的左端,质量m=0.4kg的小球乙可在光滑水平面的滑动,甲、乙两球之间因受到相互作用而具有一定的势能,相互作用力沿二者连线且随间距的变化而变化。现已测出势能随位置x的变化规律如图(b)所示中的实线所示。已知曲线最低点的横坐标x0=20cm,虚线①为势能变化曲线的渐近线,虚线②为经过曲线上x=11cm点的切线,斜率绝对值k=0.03J/ cm。
试求:(1)将小球乙从x1=8cm处由静止释放,小球乙所能达到的最大速度为多大?
(2)小球乙在光滑水平面上何处由静止释放,小球乙不可能第二次经过x0=20cm的位置?并写出必要的推断说明;
(3)小球乙经过x=11cm时加速度大小和方向。
解:
(1)球乙运动到x0=20cm位置时势能最少,速度最大,
能量守恒:![]() (2分)
(2分)
解得 ![]()
![]() (2分)
(2分)
(2)在0<x<6cm区间内将小球乙由静止释放,不可能第二次经过x0。 (2分)
原因: 在0<x<20cm区间内两球之间作用力为排斥力,在20cm <x<∞区间内两球之间作用力为吸引力,无穷远处和6cm处的势能均为0.28J。若小球乙的静止释放点在6cm <x<∞区间,小球乙将做往复运动,多次经过x0=20cm的位置。而静止释放点在0<x<6cm区间内时,初态势能大于0.28J,小球乙将会运动到无穷远处而无法返回,只能经过x0位置一次。 (3分)
(3)x3=11cm处的切线斜率绝对值k=0.03J/ cm=3J/m
表明此处乙球受到甲球F=3N的排斥力,(2分)
所以,乙球在x3=11cm处时,加速度大小 ![]() (2分)
(2分)
方向沿x轴正方向(1分)

 阅读快车系列答案
阅读快车系列答案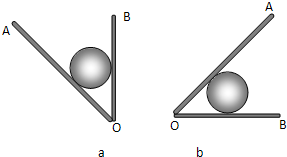 如图(a)所示,小球放置在光滑V形槽中,初始槽板OB处竖直平面,将V形槽沿顺时针绕槽底角O点缓慢转动90°,到OB处水平平面,如图(b)所示.在这个过程中,板OB受到的压力将
如图(a)所示,小球放置在光滑V形槽中,初始槽板OB处竖直平面,将V形槽沿顺时针绕槽底角O点缓慢转动90°,到OB处水平平面,如图(b)所示.在这个过程中,板OB受到的压力将 (1)(单选题)用细线将一块玻璃片水平地悬挂在弹簧测力计的下端,并使玻璃片贴在水面上,如图所示,然后用手缓慢提起弹簧测力计,在使玻璓片脱离水面的一瞬间,关于弹簧测力计的示数下列说法中正确的是
(1)(单选题)用细线将一块玻璃片水平地悬挂在弹簧测力计的下端,并使玻璃片贴在水面上,如图所示,然后用手缓慢提起弹簧测力计,在使玻璓片脱离水面的一瞬间,关于弹簧测力计的示数下列说法中正确的是

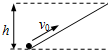 如图(a)所示,小球的初速度为v0,沿光滑斜面上滑,能上滑的最大高度为h,在图(b)中,四个物体的初速度均为v0.在A图中,小球沿一光滑内轨向上运动,内轨半径大于h;在B图中,小球沿一光滑内轨向上运动,内轨半径小于h;在图C中,小球沿一光滑内轨向上运动,内轨直径等于h;在D图中,小球固定在棒的下端,棒的长度为h的一半,小球随棒绕O点向上转动.则小球上升的高度能达到h的有( )
如图(a)所示,小球的初速度为v0,沿光滑斜面上滑,能上滑的最大高度为h,在图(b)中,四个物体的初速度均为v0.在A图中,小球沿一光滑内轨向上运动,内轨半径大于h;在B图中,小球沿一光滑内轨向上运动,内轨半径小于h;在图C中,小球沿一光滑内轨向上运动,内轨直径等于h;在D图中,小球固定在棒的下端,棒的长度为h的一半,小球随棒绕O点向上转动.则小球上升的高度能达到h的有( )