Question

在一次抗洪救灾工作中，一架直升机A用长H＝50 m的悬索(重力可忽略不计)系住一质量m＝50 kg的被困人员B，直升机A和被困人员B以v₀＝10 m/s的速度一起沿水平方向匀速运动，如图甲所示．某时刻开始收悬索将人吊起，在5 s时间内，A、B之间的竖直距离以l＝50－t²(单位：m)的规律变化，取g＝10 m/s²．

(1)求在5 s末被困人员B的速度大小及位移大小．

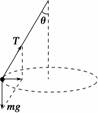
(2)直升机在t＝5 s时停止收悬索，但发现仍然未脱离洪水围困区，为将被困人员B尽快运送到安全处，飞机在空中旋转后静止在空中寻找最近的安全目标，致使被困人员B在空中做圆周运动，如图乙所示．此时悬索与竖直方向成37°角，不计空气阻力，求被困人员B做圆周运动的线速度以及悬索对被困人员B的拉力．

(sin 37°＝0.6，cos 37°＝0.8)

Answer 1

答案：
解析：

解析：(1)被困人员在水平方向上做匀速直线运动，v0＝10 m/s 　　在竖直方向上被困人员的位移y＝H－l＝50－(50－t2)＝t2， 　　所以竖直方向上做初速度为零匀加速直线运动，加速度a＝2 m/s2的， 　　被困人员5 s末在竖直方向上的速度为vy＝at＝10 m/s， 　　合速度v＝＝10m/s， 　　竖直方向上的位移y＝at2＝25 m， 　　水平方向的位移x＝v0t＝50 m， 　　合位移s＝＝25m． 　　(3)t＝5 s时悬索的长度＝50－y＝25 m，旋转半径r＝sin 37°， 　　由m＝mgtan37°，解得＝m/s．此时被困人员B的受力情况如图所示，由图可知Tcos37°＝mg，解得T＝＝625 N．