题目内容
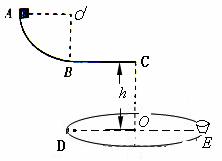
如图所示，一半径r=1m的圆盘水平放置，在其边缘 E点固定一小桶(可视为质点)。在圆盘直径 DE 的正上方平行放置一水平滑道BC ，滑道右端 C点 与圆盘圆心O在同一竖直线上，且竖直高度h = 1.25 m。AB为一竖直面内的光滑四分之一圆弧轨道，半径R=0.45m,且与水平滑道相切与B点。一质量m=0.2kg的滑块（可视为质点）从A点由静止释放，当滑块经过C点时，圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动，最终物块由C 点水平抛出，恰好落入圆盘边缘的小桶内．已知滑块与滑道 BC间的摩擦因数μ＝0.2。（取g=10m/s2）求：
（1）滑块到达B点时受到的支持力NB的大小；
（2）水平滑道 BC的长度L；
（3）圆盘转动的角速度ω应满足的条件。
（1）滑块由A点到B由动能定理得：mgR＝
mvB2 …………1分
解得：vB＝3m/s
滑块到达B点时，由牛顿第二定律得：NB－mg＝m
………… 1分
解得：NB＝6N ………………………………………1分
（2）滑块离开C后，做平抛运动： r＝vCt ………… 1分
h＝gt12 ………… 1分
解得：t=0.5s ………… 1分
；vC＝2m/s
滑块由B点到由C点的过程中由动能定理得：－μmgL＝mvC2－mvB2 …………1分
解得：L＝1.25m ………………………………………1分
（3）圆盘转动的角速度ω应满足条件：
…………2分
ω＝4nπ rad/s （n=1、2、3、4……） …………1分
练习册系列答案
星级口算天天练系列答案
相关题目
（2013?德州一模）如图所示，一半径R=1m的圆盘水平放置，在其边缘 E点固定一小桶（可视为质点）．在圆盘直径 DE 的正上方平行放置一水平滑道 BC，滑道右端 C点 与圆盘圆心O在同一竖直线上，且竖直高度 h=1.25m．AB为一竖直面内的光滑四分之一圆弧轨道，半径r=0.45m，且与水平滑道相切与B点．一质量m=0.2kg的滑块（可视为质点）从A点由静止释放，当滑块经过B点时，圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动，最终物块由C 点水平抛出，恰好落入圆盘边缘的小桶内．已知滑块与滑道 BC间的摩擦因数μ=0.2．（取g=10m/s2）求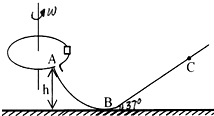
如图所示，一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动，圆盘边缘有一质量m=1.0kg的小滑块．当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，经光滑的过渡圆管（图中圆管未画出）进入轨道ABC．已知AB段为光滑的弧形轨道，A点离B点所在水平面的高度h=1.2m；BC斜面与AB轨道对接且倾角为37°，滑块与圆盘及BC斜面间的动摩擦因数均为μ=0.5，滑块在运动过程中始终未脱离轨道，不计在过渡圆管处和B点的机械能损失，设最大静摩擦力等于滑动摩擦力，取g=10m/s2，sin37°=0.6，cos37°=0.8
如图所示，一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动，圆盘边缘有一质量m=1.0kg的小滑块．当圆盘转动的角速度逐渐增大到某一数值时，滑块刚好从圆盘边缘处滑落，进入轨道ABC．已知AB段为光滑的圆弧形轨道，轨道半径r=2.5m，B点是圆弧形轨道与水平地面的相切点，A点与B点的高度差h=1.2m；倾斜轨道BC与圆轨道AB对接且倾角为37°，滑块与圆盘及BC轨道间的动摩擦因数均为μ=0.5，滑块在运动过程中始终未脱离轨道，不计滑块在A点和B点处的机械能损失，设最大静摩擦力等于滑动摩擦力，取g=10m/s2，sin37°=0.6，cos37°=0.8．
