题目内容
 如图所示,一玩滚轴溜冰的小孩(可视为质点)质量为m=30kg,他在左侧平台上滑行一段距离以3m/s的速度从平台右侧水平滑出,而后恰能无碰撞地沿圆弧切线方向从A点进入竖直面内的光滑圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平.对应圆心角θ=106°,当小孩通过圆弧最低点时,对轨道的压力大小为915N.(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)求:
如图所示,一玩滚轴溜冰的小孩(可视为质点)质量为m=30kg,他在左侧平台上滑行一段距离以3m/s的速度从平台右侧水平滑出,而后恰能无碰撞地沿圆弧切线方向从A点进入竖直面内的光滑圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平.对应圆心角θ=106°,当小孩通过圆弧最低点时,对轨道的压力大小为915N.(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)求:(1)小孩自滑离平台至进入圆弧轨道所用的时间
(2)圆弧轨道的半径.
分析:(1)小孩无碰撞进入圆弧轨道,则小孩落到A点的速度方向沿A点的切线方向,根据平抛运动的高度求出运动的时间.
(2)根据机械能守恒定律求出小孩运动到最低点时的速度,结合牛顿第二定律求出支持力的大小,从而得出小孩在最低点对轨道的压力.
(2)根据机械能守恒定律求出小孩运动到最低点时的速度,结合牛顿第二定律求出支持力的大小,从而得出小孩在最低点对轨道的压力.
解答: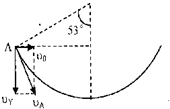 解:(1)由题意知:小孩落到A点时速度方向沿A点切线方向,小孩做平抛运动,则有 tan53°=
解:(1)由题意知:小孩落到A点时速度方向沿A点切线方向,小孩做平抛运动,则有 tan53°=
得 vy=v0tan53°=
v0=4m/s
又 vy=gt
解得时间t=0.4s
(2)设小孩到最低点的速度为vx,由机械能守恒定律得
m
-
m
=mg[h+R(1-cos53°)]
在最低点,据牛顿第二定律,有 FN-mg=m
又 h=
gt2
由以上三式解得R=2m
答:
(1)小孩自滑离平台至进入圆弧轨道所用的时间是0.4s.
(2)圆弧轨道的半径是2m.
 解:(1)由题意知:小孩落到A点时速度方向沿A点切线方向,小孩做平抛运动,则有 tan53°=
解:(1)由题意知:小孩落到A点时速度方向沿A点切线方向,小孩做平抛运动,则有 tan53°=| vy |
| v0 |
得 vy=v0tan53°=
| 4 |
| 3 |
又 vy=gt
解得时间t=0.4s
(2)设小孩到最低点的速度为vx,由机械能守恒定律得
| 1 |
| 2 |
| v | 2 x |
| 1 |
| 2 |
| v | 2 0 |
在最低点,据牛顿第二定律,有 FN-mg=m
| ||
| R |
又 h=
| 1 |
| 2 |
由以上三式解得R=2m
答:
(1)小孩自滑离平台至进入圆弧轨道所用的时间是0.4s.
(2)圆弧轨道的半径是2m.
点评:本题考查了平抛运动、圆周运动的综合,运用了机械能守恒定律、牛顿第二定律以及运动的合成等知识,综合性较强,是一道好题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
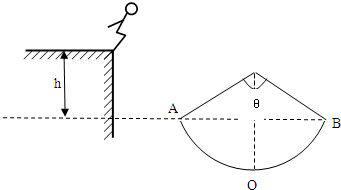 (2008?南开区模拟)如图所示,一玩滚轴溜冰的小孩(可视作质点)质量为m=30kg,他在左侧平台上滑行一段距离后平抛,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平.已知圆弧半径为R=1.0m,对应圆心角为θ=106°,平台与AB连线的高度差为h=0.8m (计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)求:
(2008?南开区模拟)如图所示,一玩滚轴溜冰的小孩(可视作质点)质量为m=30kg,他在左侧平台上滑行一段距离后平抛,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平.已知圆弧半径为R=1.0m,对应圆心角为θ=106°,平台与AB连线的高度差为h=0.8m (计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)求: