题目内容
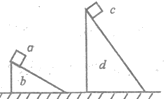
【题目】一个质量为M的箱子放在水平地面上,箱内用一段固定长度的轻质细线拴一质量为m的小球,线的另一端拴在箱子的顶板上,现把细线和球拉到左侧与竖直方向成θ角处静止释放,如图所示,在小球摆动的过程中箱子始终保持静止,则以下判断正确的是( )

A. 在小球摆动的过程中,线的张力呈周期性变化,但地面对箱子的作用力始终保持不变
B. 小球摆到右侧最高点时,箱子对地面的压力为(M+m)g,箱子受到地面向左的静摩擦力
C. 小球摆到最低点时,箱子对地面的压力大于(M+m)g,箱子不受地面的摩擦力
D. 小球摆到最低点时,小球对细线的拉力大于mg,箱子处于超重状态
【答案】C
【解析】
A.在小球向下摆动的过程中,速度越来越大,对小球受力分析根据牛顿第二定律可知:![]()
绳子在竖直方向的分力为:
![]()
当小球的速度越来越大时,角度θ越来越小,故F′越大,故箱子对地面的作用力增大,在整个运动过程中箱子对地面的作用力时刻变化,故A错误;
B.小球摆到右侧最高点时,小球有垂直于绳斜向下的加速度,对整体,由于箱子不动加速度为aM=0,a′为小球在竖直方向的加速度,根据牛顿第二定律可知:
(M+m)g-FN=MaM+ma′,
其中a′为m竖直方向的加速度,故FN小于(M+m)g,根据牛顿第三定律可知对地面的压力小于(M+m)g,此时由于小球有水平向左的加速度分量,则地面对整体有向左的摩擦力,即箱子受到地面向左的静摩擦力,故B错误;
CD.在最低点,小球受到的重力和拉力的合力提供向心力,由牛顿第二定律有:
![]()
联立解得:
![]()
则根据牛顿第三定律知,球对箱的拉力大小为:
![]()
故此时箱子对地面的压力为:
![]() ,
,
故小球摆到最低点时,箱子对地面的压力大于(M+m)g,绳对箱顶的拉力大于mg,此时箱子不受地面的摩擦力作用,箱子处于平衡状态,故C正确
D错误