题目内容
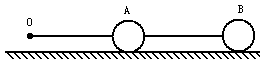
如图所示，A，B两球质量相等，固定在长为L的轻杆的中点和右端，其左端为O点．现使两球在光滑水平面上先后做沿杆向左的匀加速直线运动和绕O点的匀速圆周运动．已知A球在这两种情况下加速度大小相等，则A球先后受到的合力比为多少，OA杆先后受到的张力比为多少，AB杆先后受到的张力比为多少?
答案：
解析：
提示：
解析：
|
A，B为连接体，可由整体法和隔离法，运用牛顿第二定律求解． 当A球向左以加速度a做匀加速直线运动时，B球加速度也为a.A所受合力FA＝ma．OA杆水平张力T1，由整体法得T1＝2ma，AB杆水平张力T2，隔离B得T2＝ma，
当以O为圆心，A球以加速度a做匀速圆周运动时，A，B角速度相等，由半径关系得aB=ω2L,而a＝ω2· 故有FA/ |
，故aB=2a．由A所受合力
＝ma，由整体法得OA杆张力
＝ma+m·2a＝3ma，对B受力分析得AB杆张力
＝m·2a＝2ma．
＝1∶l，T1/
＝2∶3，T2/
＝1∶2．提示：
|
受力分析是求解动力学问题的基础，对于连接体问题可运用整体法或隔离法，结合牛顿定律，建立动力学方程．物体做匀速圆周运动时，合力指向圆心提供向心力． |
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
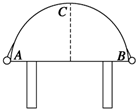如图所示，A、B两球质量分别为4m和5m，其间用轻绳连接，跨放在光滑的半圆柱体上（半圆柱体的半径为R）．两球从水平直径的两端由静止释放．已知重力加速度为g，圆周率用π表示．当球A到达最高点C时，求：
如图所示，A、B两球质量相同，悬线长度LA＞LB，将它们的悬线都拉至同一水平位置后，无初速释放，则两小球摆到最低点时：（取同一零势能参考面）（ ）
如图所示，A、B两球用细线悬挂于天花板上且静止不动，两球质量mA=2mB，两球间是一个轻质弹簧，如果突然剪断悬线，则在剪断悬线瞬间（ ）
如图所示，A、B两球用劲度系数为k1的轻弹簧相连，A被固定在竖直支架上，A点正上方的点O悬有一轻绳拉住B球，平衡时绳长为L，张力为T1．若将弹簧换成劲度系数为k2的轻弹簧，再次平衡时绳中的张力为T2，则T1、T2的关系是（ ）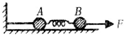
如图所示，A、B两球质量均为m，它们之间用轻弹簧连接，放在光滑的水平地面上，A球与墙之间有一不可伸长的细绳，B球受到水平向右的拉力F，A、B两球均处于静止状态．现突然撤去拉力F，此瞬间A、B的加速度aA、aB的大小是（ ）