Question

（18分）如图（甲）所示，M₁M₄、N₁N₄为平行放置的水平金属轨道，M₄P、N₄Q为相同半径，平行放置的竖直半圆形金属轨道，M₄、N₄为切点，P、Q为半圆轨道的最高点，轨道间距L=1.0m，圆轨道半径r=0.32m，整个装置左端接有阻值R=0.5Ω的定值电阻。M₁M₂N₂N₁、M₃M₄N₄N₃为等大的长方形区域Ⅰ、Ⅱ，两区域宽度 d=0.5m，两区域之间的距离s=1.0m；区域Ⅰ内分布着均匀的变化的磁场B₁，变化规律如图（乙）所示，规定竖直向上为B₁的正方向；区域Ⅱ内分布着匀强磁 场B₂，方向竖直向上。两磁场间的轨道与导体棒CD间的动摩擦因数为μ=0.2，M₃N₃右侧的直轨道及半圆形轨道均光滑。质量m=0.1kg，电阻R₀=0.5Ω的导体棒CD在垂直于棒的水平恒力F拉动下，从M₂N₂处由静止开始运动，到达M₃N₃处撤去恒力F，CD棒匀速地穿过匀强磁场区，恰好通过半圆形轨道的最高点PQ处。若轨道电阻、空气阻力不计，运动过程导棒与轨道接触良好且始终与轨道垂直，g取10m/s² 求：

（1）水平恒力F的大小；

（2）CD棒在直轨道上运动过程中电阻R上产生的热量Q；

（3）磁感应强度B₂的大小。

 

 

Answer 1

【答案】

（1F=1.0N    (2) 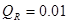J（3）B₂=0.05T

【解析】（1）CD棒在PQ处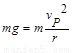： -----------①

设CD棒在匀强磁场区速度为v，则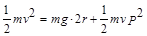----------②

CD棒在恒力F作用下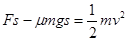：----③     

由①②③得：F=1.0N----④

(2) 棒在直轨道上运动，产生感应电流时间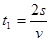--------⑤    

感应电动势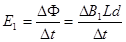------⑥

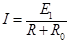----⑦    

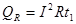------⑧  

由⑤⑥⑦⑧得 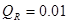 J-------⑨

（3）由于CD棒穿过匀强磁场区，此过程无感应电流，设CD棒进入M₃N₃界后的任一短时间Δt内 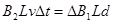 ------ ⑩    

且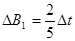----（11）  

由①②得v=4m/s-------- -（12）    

由⑩（11）（12）得  B₂=0.05T-

本题考查法拉第电磁感应定律和恒定电流的结合题，导体棒刚好从最高点飞出，可知由重力提供向心力，求出此时速度大小，再由最低点到最高点应用动能定理可求得最低点速度大小，再以水平面应用动能定理可知F大小，在磁场中导体棒切割磁感线，由E=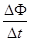可求得感应电动势大小，在由热功率公式可求得热量Q