题目内容

如图所示，物体在离斜面底端4 m处由静止滑下，若动摩擦因数均为0.5，斜面倾角为37°，斜面与平面间由一小段圆弧连接，求物体能在水平面上滑行多远。
解：物体在斜面上受重力mg、支持力N1、摩擦力f1的作用，沿斜面加速下滑(因μ＝0.5<tanθ＝0.75)，到水平面后，在摩擦力f2作用下做减速运动，直至停止

对物体在斜面上时进行受力分析，如图甲所示
下滑阶段：N1＝mgcos37°
故f1＝μN1＝μmgcos37°
由动能定理得：mgsin37°l1－μmgcos37°l1＝mv12－0 ①
在水平运动过程中受力分析如图乙所示
f2＝μN2＝μmg
由动能定理得－μmgl2＝0－mv12  ②
由①②式可得l2＝l1＝×4 m＝1.6 m
法二：对物体受力分析同上
物体运动的全过程中，初、末状态速度均为零，对全过程应用动能定理
mgsin37°l1－μmgcos37°l1－μmgl2＝0
得l2＝l1＝×4 m＝1.6 m
练习册系列答案
相关题目
如图所示，在离地高度为H的水平桌面上，一个质量为m的物体被人斜向上抛出，它到达地面时的速度大小为v，不计空气阻力，求：
（1）物体运动至水平桌面下h处的A点时，所具有的动能是多大；
（2）人对该物体做的功是多少？
（1）下列哪些因素会使“探究平抛运动的规律”实验的误差减小
BC
BC

A．使小球与斜槽间尽量光滑
B．安装斜槽时使其末端水平
C．建立坐标系时，应以小球离开斜槽末端时小球的球心为坐标原点
D．根据曲线计算平抛运动的初速度时，在曲线上取离原点O较近的点
（2）如图所示为某次实验所描绘的平抛物体运动的轨迹，A、B、C三点的坐标为A（0.35m，0.05m）、B（ 0.70m，0.20m）、C（1.05m，0.45m）．试根据以上的测量结果计算：物体做平抛运动的初速度v0为
3.5
3.5
m/s；B点竖直的速度为
4.0
4.0
m/s．（g=10m/s2，结果保留2位有效数字）
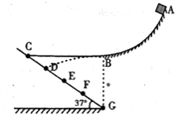精英家教网如图所示，一光滑的半圆形轨道处于竖直平面内，并和一粗糙的斜面相接，其半径大小为R=0.4m，直径BC在竖直方向上，一小物体放在斜面上的A点，离水平面高度为h=3m，小物体与斜面之间的动摩擦因数为μ=0.5，斜面倾角θ=37°．已知sin37°=0.6，cos37°=0.8，重力加速度g=10m/s2，现在把小物体从静止开始自由释放，求
（1）小物体运动到斜面底端B点时速度的大小？
（2）证明小物体可以沿半圆形轨道运动到最高点C；
（3）小物体离开半圆轨道后第一次落到斜面上时，其速度v的大小．
精英家教网如图所示，AB是光滑的斜槽，斜槽的末端B的切线水平，斜面CG的倾角θ=37°，斜面上的C点与B点在同一水平面上，G点与B点在同一竖直线上，D、E、F是光滑斜面 CG上的四等分点．现有一个质量为1kg的小物体在离B端高h=5m的A处，由静止开始沿 斜槽滑下，恰好落到斜面上的D点，物体落到D点后不再反弹，只有沿斜面方向上的速度．sin37°=0.6，cos37°=0.8，g=10m/s2．则：
（1）物体到达B点的速度大小是多少？
（2）物体落到斜面CG上时，损失的机械能是多少？

第三部分 运动学

第一讲　基本知识介绍

一． 基本概念

1．  质点

2．  参照物

3．  参照系——固连于参照物上的坐标系（解题时要记住所选的是参照系，而不仅是一个点）

4．绝对运动，相对运动，牵连运动：v绝=v相+v牵 

二．运动的描述

1．位置：r=r(t) 

2．位移：Δr=r(t+Δt)－r(t)

3．速度：v=limΔt→0Δr/Δt.在大学教材中表述为：v=dr/dt, 表示r对t 求导数

5．以上是运动学中的基本物理量，也就是位移、位移的一阶导数、位移的二阶导数。可是

三阶导数为什么不是呢？因为牛顿第二定律是F=ma,即直接和加速度相联系。（a对t的导数叫“急动度”。）

6．由于以上三个量均为矢量，所以在运算中用分量表示一般比较好

三．等加速运动

v(t)=v0+at           r(t)=r0+v0t+1/2 at2 

 一道经典的物理问题：二次世界大战中物理学家曾经研究，当大炮的位置固定，以同一速度v0沿各种角度发射，问：当飞机在哪一区域飞行之外时，不会有危险？（注：结论是这一区域为一抛物线，此抛物线是所有炮弹抛物线的包络线。此抛物线为在大炮上方h=v2/2g处，以v0平抛物体的轨迹。） 

练习题：

一盏灯挂在离地板高l2,天花板下面l1处。灯泡爆裂，所有碎片以同样大小的速度v 朝各个方向飞去。求碎片落到地板上的半径（认为碎片和天花板的碰撞是完全弹性的，即切向速度不变，法向速度反向；碎片和地板的碰撞是完全非弹性的，即碰后静止。）

四．刚体的平动和定轴转动

1． 我们讲过的圆周运动是平动而不是转动 

  2．  角位移φ=φ（t）, 角速度ω=dφ/dt , 角加速度ε=dω/dt

 3．  有限的角位移是标量，而极小的角位移是矢量

4．  同一刚体上两点的相对速度和相对加速度 

两点的相对距离不变，相对运动轨迹为圆弧，VA=VB+VAB,在AB连线上

投影：[VA]AB=[VB]AB,aA=aB+aAB,aAB=,anAB+,aτAB, ,aτAB垂直于AB,,anAB=VAB2/AB 

例：A，B，C三质点速度分别VA ，VB  ，VC      

求G的速度。

五．课后习题：

一只木筏离开河岸，初速度为V，方向垂直于岸边，航行路线如图。经过时间T木筏划到路线上标有符号处。河水速度恒定U用作图法找到在2T，3T，4T时刻木筏在航线上的确切位置。

五、处理问题的一般方法

（1）用微元法求解相关速度问题

例1：如图所示，物体A置于水平面上，A前固定一滑轮B，高台上有一定滑轮D，一根轻绳一端固定在C点，再绕过B、D，BC段水平，当以恒定水平速度v拉绳上的自由端时，A沿水平面前进，求当跨过B的两段绳子的夹角为α时，A的运动速度。

（vA＝）

（2）抛体运动问题的一般处理方法

  1. 平抛运动
  2. 斜抛运动
  3. 常见的处理方法

（1）将斜上抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动

（2）将沿斜面和垂直于斜面方向作为x、y轴，分别分解初速度和加速度后用运动学公式解题

（3）将斜抛运动分解为沿初速度方向的斜向上的匀速直线运动和自由落体运动两个分运动，用矢量合成法则求解

例2：在掷铅球时，铅球出手时距地面的高度为h，若出手时的速度为V0，求以何角度掷球时，水平射程最远？最远射程为多少？

（α=、 x=）

第二讲 运动的合成与分解、相对运动

（一）知识点点拨

  1. 力的独立性原理：各分力作用互不影响，单独起作用。
  2. 运动的独立性原理：分运动之间互不影响，彼此之间满足自己的运动规律
  3. 力的合成分解：遵循平行四边形定则，方法有正交分解，解直角三角形等
  4. 运动的合成分解：矢量合成分解的规律方法适用
    1. 位移的合成分解 B.速度的合成分解 C.加速度的合成分解

参考系的转换：动参考系，静参考系

相对运动：动点相对于动参考系的运动

绝对运动：动点相对于静参考系统（通常指固定于地面的参考系）的运动

牵连运动：动参考系相对于静参考系的运动

（5）位移合成定理：SA对地=SA对B+SB对地

速度合成定理：V绝对=V相对+V牵连

加速度合成定理：a绝对=a相对+a牵连

（二）典型例题

（1）火车在雨中以30m/s的速度向南行驶，雨滴被风吹向南方，在地球上静止的观察者测得雨滴的径迹与竖直方向成21。角，而坐在火车里乘客看到雨滴的径迹恰好竖直方向。求解雨滴相对于地的运动。

提示：矢量关系入图

答案：83.7m/s

（2）某人手拿一只停表，上了一次固定楼梯，又以不同方式上了两趟自动扶梯，为什么他可以根据测得的数据来计算自动扶梯的台阶数？

提示：V人对梯=n1/t1

      V梯对地=n/t2

      V人对地=n/t3

V人对地= V人对梯+ V梯对地

答案：n=t2t3n1/（t2-t3）t1

(3)某人驾船从河岸A处出发横渡，如果使船头保持跟河岸垂直的方向航行，则经10min后到达正对岸下游120m的C处，如果他使船逆向上游，保持跟河岸成а角的方向航行，则经过12.5min恰好到达正对岸的B处，求河的宽度。

提示：120=V水*600

        D=V船*600

 答案：200m

（4）一船在河的正中航行，河宽l=100m，流速u=5m/s，并在距船s=150m的下游形成瀑布，为了使小船靠岸时，不至于被冲进瀑布中，船对水的最小速度为多少？

提示：如图船航行

答案：1.58m/s

（三）同步练习

1.一辆汽车的正面玻璃一次安装成与水平方向倾斜角为β1=30°，另一次安装成倾角为β2=15°。问汽车两次速度之比为多少时，司机都是看见冰雹都是以竖直方向从车的正面玻璃上弹开？（冰雹相对地面是竖直下落的）

2、模型飞机以相对空气v=39km/h的速度绕一个边长2km的等边三角形飞行，设风速u = 21km/h ，方向与三角形的一边平行并与飞机起飞方向相同，试求：飞机绕三角形一周需多少时间？

3.图为从两列蒸汽机车上冒出的两股长幅气雾拖尾的照片（俯视）。两列车沿直轨道分别以速度v1=50km/h和v2=70km/h行驶，行驶方向如箭头所示，求风速。

4、细杆AB长L ，两端分别约束在x 、 y轴上运动，（1）试求杆上与A点相距aL（0＜ a ＜1)的P点运动轨迹；（2）如果vA为已知，试求P点的x 、 y向分速度vPx和vPy对杆方位角θ的函数。

（四）同步练习提示与答案

1、提示：利用速度合成定理，作速度的矢量三角形。答案为：3。

2、提示：三角形各边的方向为飞机合速度的方向（而非机头的指向）；

第二段和第三段大小相同。

参见右图，显然：

v2 =  + u2 － 2v合ucos120°

可解出 v合 = 24km/h 。

答案：0.2hour（或12min.）。

3、提示：方法与练习一类似。答案为：3

4、提示：（1）写成参数方程后消参数θ。

（2）解法有讲究：以A端为参照， 则杆上各点只绕A转动。但鉴于杆子的实际运动情形如右图，应有v牵 = vAcosθ，v转 = vA，可知B端相对A的转动线速度为：v转 + vAsinθ=  。

P点的线速度必为  = v相 

所以 vPx = v相cosθ+ vAx ，vPy = vAy － v相sinθ

答案：（1） +  = 1 ，为椭圆；（2）vPx = avActgθ ，vPy =（1 － a）vA

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网