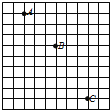
��Ŀ����
����Ŀ����ͼ����ʾ����y���Ҳ���д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B=1T����ԭ��O����ڢ�������һ�Ⱥ� ![]() =1��104C/kg�Ĵ���������ӣ��������ƣ����ٶȴ�С��0=103m/s������ֱ�ڴų�����x���������30��ǣ�
=1��104C/kg�Ĵ���������ӣ��������ƣ����ٶȴ�С��0=103m/s������ֱ�ڴų�����x���������30��ǣ�
��1���������ڸ���ǿ�ų���������Բ���˶��İ뾶R���ڸôų����˶���ʱ��t1 ��
��2�����ų���ʱ��仯�Ĺ�����ͼ����ʾ����ֱ��ֽ������Ϊ������ ![]() s��ռ䲻���ڴų�����t=0ʱ�̣������Դ�O������ԭ����ͬ���ٶȦ�0���룬�����Ӵ�O��������2�ξ���x��ʱ�����꣮
s��ռ䲻���ڴų�����t=0ʱ�̣������Դ�O������ԭ����ͬ���ٶȦ�0���룬�����Ӵ�O��������2�ξ���x��ʱ�����꣮
���𰸡�
��1���⣺�켣��ͼ����ʾ���� ![]() ��
��

�켣�뾶 ![]()
�����˶�����T= ![]() =2�С�10��4s
=2��10��4s
�����ڴų��й켣���Ե�Բ�Ľ�Ϊ240�㣬
���������ڴų����˶���ʱ��Ϊt1= ![]() =
= ![]()
���������ڸ���ǿ�ų���������Բ���˶��İ뾶Rδ0.1m���ڸôų����˶���ʱ��t1Ϊ ![]() ��
��
��2���⣺�ų��仯�İ�����Ϊ ![]()
��ͼ���У���OO1C=��CO2D=120�㣬��O1O2ƽ����x��
OE=2��R+Rsin30�㣩=3R=0.3m
Rt��EDP�У���EDP=60�㣬DE=2Rsin60��
EP=DEtan60��=3R=0.3m
�����Ӵ�O��������2�ξ���x��ʱ������xp=OE+EP=0.6m

�����ų���ʱ��仯�Ĺ�����ͼ����ʾ����ֱ��ֽ������Ϊ������ ![]() s��ռ䲻���ڴų�����t=0ʱ�̣������Դ�O������ԭ����ͬ���ٶȦ�0���룬���Ӵ�O��������2�ξ���x��ʱ������Ϊ0.6m��
s��ռ䲻���ڴų�����t=0ʱ�̣������Դ�O������ԭ����ͬ���ٶȦ�0���룬���Ӵ�O��������2�ξ���x��ʱ������Ϊ0.6m��
����������1���������������������ڴų����˶�ʱ��ķ���������������������Ȼ������˶��켣����ϼ��ι�ϵ������Բ�Ľ��������ڹ�ʽ����˶�ʱ�䡣
��2�����������˶��Ĺ켣�����Բ�Ľ����ü��ι�ϵ���ٽ�����ӵİ뾶���x���ϵ�λ�����ꡣ