题目内容
3.某同学验证机械能守恒定律时,设计了如图1所示的实验装置.
(1)实验中,先不挂钩码,将木板倾斜一定角度,让小车拖着纸带匀速下滑.判断小车匀速的方法是:逐步调节木板的倾斜程度,给小车一初速度,让拖着纸带的小车下滑,直到小车后面的纸带上的点应为均匀分布..
(2)实验中得到了一条纸带如图2所示,选择点迹清晰且便于测量的连续7个点(标号0~6),测出0到1、2、3、4、5、6点的距离分别为d1、d2、d3、d4、d5、d6,打点周期为T;若测得小车质量为M、钩码质量为m,打点1和点5时小车的速度分别用v1、v5表示,已知重力加速度为g,则用点1与点5间运动来验证系统机械能守恒的关系式可表示为mg(d5-d1)=$\frac{1}{2}$(m+M)(${v}_{5}^{2}$-${v}_{1}^{2}$)(用题中所给字母表示).
(3)在实验数据处理时,如果以$\frac{{v}^{2}}{2}$为纵轴,以d为横轴,根据实验数据绘出$\frac{{v}^{2}}{2}$-d图象,其图线的斜率所表示的物理量的表达式为$\frac{m}{m+M}$g(用题中所给字母表示).
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出点2的瞬时速度,抓住系统重力势能的减小量等于动能的增加量列出表达式.
根据系统机械能守恒得出$\frac{{v}^{2}}{2}$与d的关系式,结合关系式得出图线斜率的物理意义.
解答 解:(1)实验中,先不挂钩码,将木板倾斜一定角度,让小车拖着纸带匀速下滑.判断小车匀速的方法是:逐步调节木板的倾斜程度,给小车一初速度,让拖着纸带的小车下滑,直到小车后面的纸带上的点应为均匀分布.
(2)点2的瞬时速度v2=$\frac{{{d}_{3}-d}_{1}}{2T}$.
验证点1与点5间系统的机械能守恒,系统重力势能的减小量为:△Ep=mg(d5-d1),
系统动能的增加量△Ek=$\frac{1}{2}$(m+M)(${v}_{5}^{2}$-${v}_{1}^{2}$),则系统机械能守恒的表达式为mg(d5-d1)=$\frac{1}{2}$(m+M)(${v}_{5}^{2}$-${v}_{1}^{2}$);
(3)根据mgd=$\frac{1}{2}$(m+M)v2得:$\frac{{v}^{2}}{2}$=$\frac{m}{m+M}$gd,
则图线的斜率k=$\frac{m}{m+M}$g.
故答案为:(1)逐步调节木板的倾斜程度,给小车一初速度,让拖着纸带的小车下滑,直到小车后面的纸带上的点应为均匀分布.
(2)mg(d5-d1)=$\frac{1}{2}$(m+M)(${v}_{5}^{2}$-${v}_{1}^{2}$);
(3)$\frac{m}{m+M}$g.
点评 解决本题的关键知道实验的原理,即验证系统重力势能的减小量和系统动能的增加量是否相等;得出图线的斜率前提是根据系统机械能守恒得出$\frac{{v}^{2}}{2}$与d的关系式.

 口算能手系列答案
口算能手系列答案| A. | 1865年麦克斯韦提出光是电磁波的一种形态 | |
| B. | 1801年托马斯•杨在实验室成功观察到了光的衍射 | |
| C. | 1818年泊松通过实验发现了圆板衍射的“泊松亮斑” | |
| D. | 1905年爱因斯坦在广义相对论中提出光速不变原理 |
 如图为长虹电视机电源部分的滤波电路,从输入端输入含有直流成分、交流低频成分的电流后,下列关于其工作原理及各电容和电感作用的说法,正确的是( )
如图为长虹电视机电源部分的滤波电路,从输入端输入含有直流成分、交流低频成分的电流后,下列关于其工作原理及各电容和电感作用的说法,正确的是( )| A. | 由于电容C1的“通直流、隔交流”的功能,电流中的交流成分被衰减 | |
| B. | 线圈L有“通交流、阻直流”的功能,直流成分和一小部分交流通过L | |
| C. | 由于电容C2的“通交流、隔直流”的功能,C2进一步滤除电流中残余的交流成分 | |
| D. | 输出端输出较稳定的交流电,这个交流电供电视机内芯正常工作 |
| A. | 作用力做正功时,反作用力一定做负功 | |
| B. | 一对作用力和反作用力的功一定大小相等,正负相反 | |
| C. | 滑动摩擦力一定对物体做负功 | |
| D. | 一对作用力和反作用力的冲量一定大小相等,方向相反 |
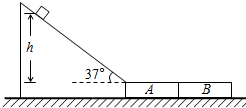 如图所示,某货场需要将质量为m=10kg的货物(可视为质点)从高处运送到地面,现利用固定在地面上的倾斜轨道传递货物,使货物由轨道顶端无初速度滑下,轨道与水平面成θ=37°角.地面上紧靠轨道依次排放两块完全相同的木板A,B,长度均为l=1.6米,厚度不计,质量为m=10kg,木板上表面与轨道末端平滑连接.货物与倾斜轨道间动摩擦因数为μ0=0.125,货物与木板间的动摩擦因数μ1,木板与地面间的动摩擦因μ2=0.2.
如图所示,某货场需要将质量为m=10kg的货物(可视为质点)从高处运送到地面,现利用固定在地面上的倾斜轨道传递货物,使货物由轨道顶端无初速度滑下,轨道与水平面成θ=37°角.地面上紧靠轨道依次排放两块完全相同的木板A,B,长度均为l=1.6米,厚度不计,质量为m=10kg,木板上表面与轨道末端平滑连接.货物与倾斜轨道间动摩擦因数为μ0=0.125,货物与木板间的动摩擦因数μ1,木板与地面间的动摩擦因μ2=0.2. 如图所示,黑箱内有导线、定值电阻和两只电压恒定的电池组成的电路.今用R=10Ω的电阻分别接在1、2和3、4之间,测得电流I12=0.4A,I34=0;而将此电阻R分别接在其它任意两点之间时,通过R的电流均为I=0.1A,画出有关电路图(标出元件的参数)
如图所示,黑箱内有导线、定值电阻和两只电压恒定的电池组成的电路.今用R=10Ω的电阻分别接在1、2和3、4之间,测得电流I12=0.4A,I34=0;而将此电阻R分别接在其它任意两点之间时,通过R的电流均为I=0.1A,画出有关电路图(标出元件的参数)
 如图所示,在竖直平面内有平面直角坐标系xoy,x轴沿水平方向,y轴沿竖直方向.空间有平行于坐标平面的匀强电场,场强方向与x轴负向成60°角、与y轴正向成30°角.两完全相同带正电小球a和b同时从坐标原点O出发,a的初速度va沿与x轴负向成30°角、与y轴正向成60°角方向,b的初速度vb沿与y轴正向成30°角、与x轴正向成60°角方向.a出发后沿直线运动到M点,当a到达M时,b正好到达y轴上的P点,MP连线平行于x轴.已知带电小球质量为m,带电量为q,重力加速度为g,两带电小球之间的相互作用忽略不计.试求:
如图所示,在竖直平面内有平面直角坐标系xoy,x轴沿水平方向,y轴沿竖直方向.空间有平行于坐标平面的匀强电场,场强方向与x轴负向成60°角、与y轴正向成30°角.两完全相同带正电小球a和b同时从坐标原点O出发,a的初速度va沿与x轴负向成30°角、与y轴正向成60°角方向,b的初速度vb沿与y轴正向成30°角、与x轴正向成60°角方向.a出发后沿直线运动到M点,当a到达M时,b正好到达y轴上的P点,MP连线平行于x轴.已知带电小球质量为m,带电量为q,重力加速度为g,两带电小球之间的相互作用忽略不计.试求: