在如图1所示的区域里.存在指向纸外的磁感应强度为B=2πmq的匀强磁场,在竖直方向存在随时间交替变化的如2所示的匀强电场.电场大小E0=mgq.已知竖直向上为正方向．一倾角为θ长度足够的光滑绝缘斜面竖直放置其中．斜面上一带正电小球从t=0时刻由静止沿斜面滑下．设第一秒内小球不会脱离斜面.求:两秒内小球离开斜面的最大距离．题目和参考答案——青夏教育精英家教网—

题目内容

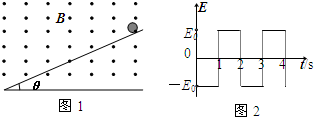
在如图1所示的区域里，存在指向纸外的磁感应强度为B=

2πm

的匀强磁场；在竖直方向存在随时间交替变化的如2所示的匀强电场，电场大小E₀=

，已知竖直向上为正方向．一倾角为θ长度足够的光滑绝缘斜面竖直放置其中．斜面上一带正电小球（质量m 带电量q）从t=0时刻由静止沿斜面滑下．设第一秒内小球不会脱离斜面，求：两秒内小球离开斜面的最大距离．

分析：在第一秒内，电场力方向竖直向下，洛伦兹力方向垂直斜面向上，小球的合力沿斜面向下，做匀加速直线运动，根据牛顿第二定律求出加速度的大小，从而求出1s末的速度，第二秒内，电场力与重力平衡，小球受洛伦兹力做匀速圆周运动，当小球运动半个周期时，距离斜面最远．结合半径公式求出最远距离．

解答：解：在第一秒内，小球在斜面上作匀加速度直线运动
由qE=mg 得
加速度a=

(mg+qE)sinθ

=2gsinθ---①
1秒末的速度V₁=2gsinθ---②
在第二秒内，小球作匀速圆周运动，由题意知周期为1秒．
r=

mv1

所以离斜面的最远距离为s=2r=

2mv1

2gSinθ

---③
答：两秒内小球离开斜面的最大距离为

2gSinθ

．

点评：本题考查小球在复合场中的运动，关键理清小球在第1s内和第2s内的运动规律，结合牛顿第二定律和运动学公式进行求解．

练习册系列答案

相关题目

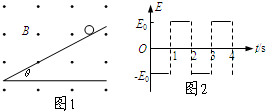在如图1所示的区域里，存在垂直指相纸外的磁感应强度为B=2πm/q的匀强磁场；在竖直方向存在随时间交替变化的如图2所示的匀强电场，场强大小E₀=mg/q，设竖直向上为正方向．一倾角为θ且足够长的光滑绝缘斜面竖直放置其中．斜面上一带正电小球（质量为m，电量为q）从t=0时刻开始沿斜面无初速滑下．设第一秒内小球不会脱离斜面，求：
（1）第1s内小球的位移．
（2）前两秒内小球离开斜面的最大距离．

在如图 9 所示的装置中 , 虚线框内存在互相垂直的匀强磁场和匀强电场 , 匀强磁场方向向下 , 磁感应强度为B₁; 匀强电场方向垂直纸面向外 , 场强为 E 。在MN右侧有垂直纸面向里的匀强磁场 , 磁感应强度为 B₂ 。现有一离子从 0₁ 点垂直于电场、磁场方向射人后 , 沿直线运动至 0₂ 点后进入MN的右侧区域 , 最后打在MN上距O₂为 d 的 P 点。不计离子的重力 , 求 :

(1)离子带何种电?

(2) 离子的电荷量与质量之比。

(3)离子在MN右侧运动的时间。

在如图甲所示的装置中，阴极K能够连续不断地发射初速不计的电子，这些电子经P、K间的电场加速后，都能通过P板上的小孔沿垂直于P板的方向进入P板右侧的区域，打到P板右侧L远处且与P平行的荧光屏Q上的O点，由于P、K相距很近，所有电子通过电场所用时间忽略不计。现在P与Q间加垂直纸面向里的匀强磁场，且从某一时刻t=0开始，在P、K间加一周期性变化的电压，电压随时间的变化关系如图乙所示，则从该时刻起，所有从小孔射出的电子恰好能全部打到荧光屏上。已知电子质量为m，带电量为e，粒子在磁场中做圆周运动的周期小于4T₀，求：

（1）电子打到荧光屏上的范围；
（2）从t=0时刻开始在电压变化的一个周期内，打到屏上距O点最近的电子与最远的电子的时间

在如图甲所示的区域里，存在指向纸外的磁感应强度为B=2πm/q的匀强磁场；在竖直方向存在随时间交替变化的如图乙所示的匀强电场，电场大小E₀=mg/q，已知竖直向上为正方向.一倾角为θ长度足够的光滑绝缘斜面竖直放置其中，斜面上一带正电小球(质量为m，带电量为q)从t=0时刻由静止开始沿斜面滑下.设第1秒内小球不会脱离斜面，求：

(1)第1秒末小球的速度.

(2)第2秒内小球离开斜面的最大距离.

(3)第5秒内带电小球不离开斜面则斜面倾角θ应满足的条件.

试题分类