题目内容
 如图所示,轻绳通过光滑的定滑轮与放在光滑的斜面上的木块m相连,斜面高h,斜面倾角θ(<30°),另一端和套在光滑竖直杆上的铁块M相连,竖直杆与斜面间的距离为
如图所示,轻绳通过光滑的定滑轮与放在光滑的斜面上的木块m相连,斜面高h,斜面倾角θ(<30°),另一端和套在光滑竖直杆上的铁块M相连,竖直杆与斜面间的距离为| 3 |
分析:以两个物体组成的系统为研究对象,只有重力对系统做功,其机械能守恒,列出等式求出铁块滑到地面时木块的速度的大小.
解答:解:以两个物体组成的系统为研究对象,只有重力对系统做功,其机械能守恒,
系统机械能守恒:
m
+
M
=Mgh-mg(2h-
h)sinθ
车拉木块模型:v1=v2sin30°
解得:v1=
答:铁块滑到地面时木块的速度的大小是
.
系统机械能守恒:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 3 |
车拉木块模型:v1=v2sin30°

解得:v1=
|
答:铁块滑到地面时木块的速度的大小是
|
点评:本题是绳系的系统机械能守恒问题,由速度分解和机械能守恒定律及几何知识结合求解,难度适中.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
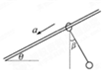 如图所示,一固定光滑杆与水平方向夹角为θ,将一质量为m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,小环与小球保持相对静止以相同的加速度a一起下滑,此时绳子与竖直方向夹角为β,则下列说法正确的是( )
如图所示,一固定光滑杆与水平方向夹角为θ,将一质量为m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,小环与小球保持相对静止以相同的加速度a一起下滑,此时绳子与竖直方向夹角为β,则下列说法正确的是( ) 如图所示,距水平地面高为h=0.4m处,水平固定一根长直光滑杆,杆上P点固定一可绕水平轴无摩擦转动且不计大小的定滑轮,一半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,杆和半圆形轨道在同一竖直面内,杆上套有一质量m=2kg小球A,半圆形轨道上套有一质量也为m=2kg的小球B,两球用一条不可伸长的轻绳通过定滑轮连接,且均可看作质点,现给小球A施加一个水平向右的恒力F=55N,g取10m/s2.求:
如图所示,距水平地面高为h=0.4m处,水平固定一根长直光滑杆,杆上P点固定一可绕水平轴无摩擦转动且不计大小的定滑轮,一半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,杆和半圆形轨道在同一竖直面内,杆上套有一质量m=2kg小球A,半圆形轨道上套有一质量也为m=2kg的小球B,两球用一条不可伸长的轻绳通过定滑轮连接,且均可看作质点,现给小球A施加一个水平向右的恒力F=55N,g取10m/s2.求: (2010?浙江模拟)如图所示,一同定光滑杆与水平方向夹角θ,将一质量m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,环与小球保持相对静止以相同的加速度a-起下滑,此时绳子与竖直方向夹角β,下列说法正确的是( )
(2010?浙江模拟)如图所示,一同定光滑杆与水平方向夹角θ,将一质量m1的小环套在杆上,通过轻绳悬挂一个质量为m2的小球,静止释放后,环与小球保持相对静止以相同的加速度a-起下滑,此时绳子与竖直方向夹角β,下列说法正确的是( ) 现要通过实验验证机械能守恒定律.实验装置如图所示:水平桌面上固定一倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的砝码相连;遮光片两条长边与导轨垂直;导轨上B点有一光电门,可以测试遮光片经过光电门时的挡光时间t,用d表示A点到导轨低端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,s表示A,B 两点的距离,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度.用g表示重力加速度.若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片与砝码组成的系统重力势能的减小量可表示为
现要通过实验验证机械能守恒定律.实验装置如图所示:水平桌面上固定一倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的砝码相连;遮光片两条长边与导轨垂直;导轨上B点有一光电门,可以测试遮光片经过光电门时的挡光时间t,用d表示A点到导轨低端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,s表示A,B 两点的距离,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度.用g表示重力加速度.若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片与砝码组成的系统重力势能的减小量可表示为
