题目内容
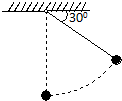 如图,长为L的细绳一端固定,另一端连接一质量为m的小球,现将球拉至与水平方向成30°角的位置释放小球(绳刚好拉直),求小球摆至最低点时的速度大小和摆球受到的绳的拉力大小.
如图,长为L的细绳一端固定,另一端连接一质量为m的小球,现将球拉至与水平方向成30°角的位置释放小球(绳刚好拉直),求小球摆至最低点时的速度大小和摆球受到的绳的拉力大小.分析:小球向下摆动的过程中,绳子的拉力不做功,只有重力做功,机械能守恒,根据机械能守恒定律可求解小球摆至最低点时的速度大小.
摆球经过最低点时,由重力和绳子的拉力的合力提供向心力,根据牛顿第二定律求解.
摆球经过最低点时,由重力和绳子的拉力的合力提供向心力,根据牛顿第二定律求解.
解答:解:由机械能守恒定律有mg(L-Lsin30°)=
mv2
得:小球摆至最低点时的速度大小v=
又在最低点,根据牛顿第二定律得 T-mg=m
得T=2mg
答:小球摆至最低点时的速度大小是
,摆球受到的绳的拉力大小是2mg.
| 1 |
| 2 |
得:小球摆至最低点时的速度大小v=
| gL |
又在最低点,根据牛顿第二定律得 T-mg=m
| v2 |
| r |
得T=2mg
答:小球摆至最低点时的速度大小是
| gL |
点评:本题机械能守恒和向心力知识的综合应用,判断机械能守恒、确定向心力来源是关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
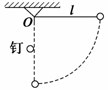
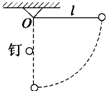 如图,长为l的细绳一端固定在O点,另一端拴住一个小球,在O点的正下方与O点相距
如图,长为l的细绳一端固定在O点,另一端拴住一个小球,在O点的正下方与O点相距| 1 |
| 2 |
| A、钉上钉子比不钉钉子,绳子更容易断 |
| B、不钉钉子比钉上钉子,绳子更容易断 |
| C、小球的线速度突然增大 |
| D、小球的角速度保持不变 |