题目内容
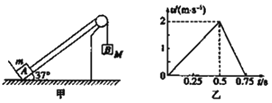
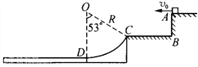
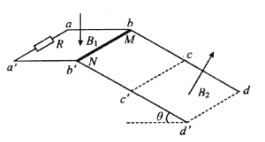
【题目】如图所示，两光滑平行金属导轨
，
之间接一阻值为
的定值电阻，
之间处于断开状态，
部分为处于水平面内，且
，
部分为处于倾角为
的斜面内，
。区域存在一竖直向下的磁场
，其大小随时间的变化规律为
（
为大于零的常数）；
区域存在一垂直于斜面向上的大小恒为
的磁场。一阻值为
、质量为
的导体棒
垂直于导轨从
处由静止释放。不计导轨的电阻，重力加速度为
。求：
(1)导体棒到达
前瞬间，电阻上消耗的电功率；
(2)导体棒从到达的过程中，通过电阻的电荷量；
(3)若导体棒到达立即减速，到达时合力恰好为零，求导体棒从到运动的时间。
【答案】（1）
（2）
（3）
（式中
【解析】
（1）因磁场
随时间的变化规律为
，所以
，
所组成回路产生的感应电动势
流过电阻
的电流
电阻消耗的功率
联立以上各式求得
（2）电阻的电荷量
根据牛顿第二定律
导体棒从
从
到达
中，通过的位移
联立解得
（3）根据（2）问，求得导体棒到达时的速度
到达
时合力为0，则
解得：
导体棒从到达过程中，运用动量定理
从到达过程中，流过导体棒的电荷量
联立以上式子，求得
（式中，）
练习册系列答案
相关题目
