题目内容
(18分)有一个长方体形的匀强磁场和匀强电场区域，它的截面是边长Ｌ＝0.20ｍ的正方形，其电场强度为Ｅ＝4×10５V／m，磁感强度Ｂ＝2×10－2Ｔ，磁场方向垂直纸面向里，当一束质荷比为
＝4×10－10kg／C的正离子流，以一定的速度从电磁场的正方形区域的边界中点射入，如右图所示，不计正离子的重力.
（1）要使离子流穿过电磁场区域而不发生偏转，电场强度的方向如何?离子流的速度多大?
（2）在离电磁场区域右边界D=0.4ｍ处有与边界平行的平直荧光屏．若撤去电场，离子流击中屏上ａ点；若撤去磁 场，离子流击中屏上ｂ点，求ab间的距离．
(18分)
解：（1）电场方向竖直向下（2分），与磁场构成粒子速度选择器，离子运动不偏转，则：
ｑＥ＝ｑＢｖ①（2分）
由①式解得：ｖ＝2×10７（ｍ／ｓ）（2分）
（2）撤去电场，离子在磁场中做匀速圆周运动，所需向心力为洛伦兹力，于是：
ｑＢｖ＝
②（1分）
由②式可得：Ｒ＝0.4（ｍ）
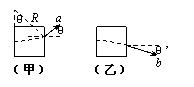
离子离开磁场区边界时，如答图（甲）所示，偏转角: sinθ ＝
=
③（1分）
由③式得：θ＝30°
偏离距离ｙ１＝Ｒ－Rcos④（1分）
由④式得：ｙ１＝0.05(ｍ)
离开磁场后离子做匀速直线运动，总的偏离距离为ｙ＝ｙ１＋Ｄtgθ⑤（1分）
由⑤式得：ｙ＝0.28(ｍ)
若撤去磁场，离子在电场中做匀变速曲线运动
通过电场的时间:ｔ＝
⑥（1分）
加速度:ａ＝
⑦（1分）
偏离距离为ｙ２′＝at２⑧（1分）
由⑥⑦⑧式解得ｙ２′＝0.05（ｍ）
偏转角为θ′，如图（乙）所示，则tgθ′＝
⑨（1分）
而vy = at ⑩（1分）
离开电场后离子做匀速直线运动，总的偏离距离
ｙ′＝ｙ２′＋Ｄｔｇθ′
（1分）
由式解得ｙ′＝0.25（ｍ）
ａ、ｂ间的距离
＝ｙ+ｙ′
（1分）
由上述式子解得：＝0.53（ｍ）（1分）
期末1卷素质教育评估卷系列答案
时（其中μ为工件与皮带之间的动摩擦因素），才有相对静止的过程，否则没有。
= 
（2）
。
。）
= m1
+ m2
+ m3
+ … + mn
只能是系统外力的矢量和，等式右边也是矢量相加。
x 。
Mg ，其中l＜L ，则x＜(L-l)的右段没有张力，x＞(L-l)的左端才有张力。
Mg时（μ为棒与平面的摩擦因素，l为小于L的某一值，M为棒的总质量），当x＜(L-l)，N≡0 ；当x＞(L-l)，N = 
〔x -〈L-l〉〕。
。
= m2a
g
。
= m1
+ m2
+ m3
+ … + mn
，猫和棒的系统外力只有两者的重力，竖直向下，而猫的加速度a1 = 0 ，所以：
g 。
。
求a1 。
。
at2 ②
a1xt2 ③
+ 
* = m 
（注：
*为惯性力），此题极简单。过程如下——
a相 t2 （3）