题目内容
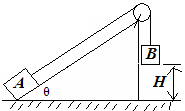
（10分)如图，已知斜面倾角300，物体A质量mA=0.4kg，物体B质量mB=0.7kg，H=0.5m。B从静止开始和A一起运动，B落地时速度v=2m/s。若g取10m/s2，绳的质量及绳的摩擦不计，求：
（1）物体与斜面间的动摩擦因数
（2）物体沿足够长的斜面滑动的最大距离
【答案】
（1）μ=0.17 （2）21/26m
【解析】分别对A和B进行受力分析，如图。
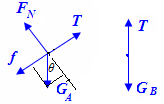
（1）对A、B列运动方程，对A有：
T – mAgsinθ-f=mAa1 ; FN=mAgcosθ ; f=μFN
对B有：mBg-T=mBa1
整合以上各式得： mBg-mBa - mAgsinθ - μmAgcosθ=ma1 (1)
对B的运动情况，有：v2=2a1H (2)
由（1）（2）代入数据得a1=4m/s2, μ=0.17
（2）B落地后，绳子松弛，不再对A有拉力T的作用，此时A有mAgsinθ+f=mAa2 ；FN=mAgcosθ ; f=μFN 整理得： a2=6.5m/s2，方向沿斜面向下，因此A继续沿斜面向上做匀减速运动，位移为x=v2/2a2=4/13m。物体沿斜面滑动的最大距离为s=x+H=21/26m
本题考查对牛顿第二定律的应用，分别以A、B为研究对象分析受力情况，建立直角坐标系，列牛顿第二定律方程，求得加速度和动摩擦因数，B落地后绳子松弛，A在重力沿斜面向下的分力和摩擦力的共同作用下沿斜面向上匀减速直线运动，先由牛顿第二定律求得加速度，再由匀减速直线运动求得位移大小
练习册系列答案
阅读快车系列答案
相关题目
北京时间2008年9月25日21时10分许，“神舟七号”在酒泉卫星发射中心载人航天发射场由“长征二号F”运载火箭发射升空，点火后583秒时，飞船与火箭在高度约200公里处成功分离．它首先进入椭圆轨道I，绕行5圈后，在椭圆轨道的远地点Q处变轨，进入圆轨道II运行，并于3天后在我国内蒙古中部草原安全着陆，其部分运行轨迹如图．已知地球半径为R，地球表面处的重力加速度为g，“神舟七号”的质量为m，椭圆轨道的近地点P离地面高为hl，“神舟七号”到达近地点P时的速率为V1，远地点Q离地面高为h2，变轨前“神舟七号”运行到椭圆轨道的远地点Q时的速率为V2，则运行到椭圆轨道的近地点P时的加速度为
冲上圆弧轨道，已知圆弧轨道的质量M=3m，不计摩擦和空气阻力，