Question

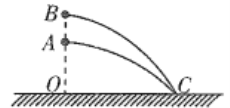
【题目】如图所示，宽度为L、足够长的匀强磁场的磁感应强度大小为B，方向垂直纸面向里．绝缘长薄板MN置于磁场的右边界，粒子打在板上时会被反弹(碰撞时间极短)，反弹前后竖直分速度不变，水平分速度大小不变、方向相反．磁场左边界上O处有一个粒子源，向磁场内沿纸面各个方向发射质量为m、电荷量为＋q、速度为v的粒子，不计粒子重力和粒子间的相互作用，粒子电荷量保持不变。

(1)要使粒子在磁场中运动时打不到绝缘薄板，求粒子速度v满足的条件；

(2)若v＝，一些粒子打到绝缘薄板上反弹回来，求这些粒子在磁场中运动时间的最小值t；

(3)若v＝，求粒子从左边界离开磁场区域的长度s。

Answer 1

【答案】（1）；（2）；（3）4

【解析】

(1)设粒子在磁场中运动的轨道半径为r1，则有

qvB＝m

如图(1)所示，

要使粒子在磁场中运动时打不到绝缘薄板，应满足

2r1＜L

解得

v＜

(2)粒子在磁场中圆周运动的周期

T＝

设运动的轨道半径为r2，则

qvB＝m

解得

r2＝L

在磁场中运动时间最短的粒子通过的圆弧对应的弦长最短，粒子运动轨迹如图(2)所示，

由几何关系可知最小时间

t＝2×

解得

t＝

(3) 设粒子的磁场中运动的轨道半径为r3，则有

qvB＝m

解得

r3＝2L

粒子在磁场中运动从左边界离开磁场，离O点最远的粒子运动轨迹如图(3)所示

则从左边界离开磁场区域的长度

s＝4r3sin 60°

解得

s＝4L