题目内容
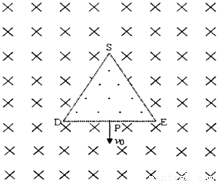
如图所示,在纸面内有一边长为L的等边三角形DES (虚线),三角形内只有方向垂直纸面向外的匀强磁场,三角形外部的足够大空间只有方向垂直纸面向里的匀强磁场,磁感应强度大小均为B虚线三角形DES为内外磁场的理想边界.一电量为+q、质量为m的带正电粒子从DE边中点P以速度V垂直DE边射入三角形外部磁场,不计粒子的重力和一切阻力,试求:(1)要使粒子能垂直DE返回到P点,从P点射出时的速度v为多大?
(2)满足(1)问的粒子第一次从P点射入外部磁场到再次返回到P点仍射入外部磁场的最短时间为多少?
【答案】分析:(1)从P点射出的粒子做圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律可求出轨迹半径R与速度的关系式.要使粒子能垂直DE返回到P点,应满足: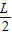 =(2n+1)R,(n=0,1,2,3…),联立解得,速度v应满足的条件
=(2n+1)R,(n=0,1,2,3…),联立解得,速度v应满足的条件
(2)在磁场中粒子做圆周运动的周期T=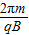 ,与粒子速度无关,粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,当R=
,与粒子速度无关,粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,当R=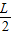 时时间最短.即可求出最短时间.
时时间最短.即可求出最短时间.
解答:解:(1)从P点射出的粒子做圆周运动,设粒子的运动半径为R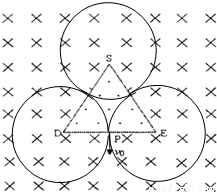
即 qvB=m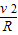
粒子返回到P点应满足: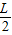 =(2n+1)R,(n=0,1,2,3…)
=(2n+1)R,(n=0,1,2,3…)
解以上各式得粒子的速度为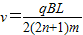 (n=0,1,2,3…)
(n=0,1,2,3…)
(2)在磁场中粒子做圆周运动的周期T=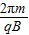 ,与粒子速度无关,所以粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,
,与粒子速度无关,所以粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,
即当:R=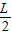 时时间最短.
时时间最短.
由轨迹图可知,粒子以三角形的三个顶点为圆心做6个圆弧运动,
其中三个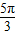 和三个
和三个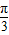 的圆弧
的圆弧
故最短时间为:t=3T=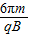
答:
(1)要使粒子能垂直DE返回到P点,从P点射出时的速度v为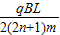 (n=0,1,2,3…).
(n=0,1,2,3…).
(2)满足(1)问的粒子第一次从P点射入外部磁场到再次返回到P点仍射入外部磁场的最短时间为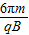 .
.
点评:本题的难点在于几何图象的确定,要抓住三角形内外圆半径关系,则可得出各自圆弧所对应的圆心角,从而确定粒子运动所经历的时间.
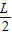 =(2n+1)R,(n=0,1,2,3…),联立解得,速度v应满足的条件
=(2n+1)R,(n=0,1,2,3…),联立解得,速度v应满足的条件(2)在磁场中粒子做圆周运动的周期T=
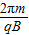 ,与粒子速度无关,粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,当R=
,与粒子速度无关,粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,当R=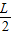 时时间最短.即可求出最短时间.
时时间最短.即可求出最短时间.解答:解:(1)从P点射出的粒子做圆周运动,设粒子的运动半径为R

即 qvB=m
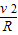
粒子返回到P点应满足:
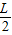 =(2n+1)R,(n=0,1,2,3…)
=(2n+1)R,(n=0,1,2,3…)解以上各式得粒子的速度为
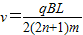 (n=0,1,2,3…)
(n=0,1,2,3…)(2)在磁场中粒子做圆周运动的周期T=
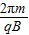 ,与粒子速度无关,所以粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,
,与粒子速度无关,所以粒子做圆周运动回旋圆弧个数越少,时间越短,当n=0时运动的时间最短,即当:R=
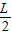 时时间最短.
时时间最短.由轨迹图可知,粒子以三角形的三个顶点为圆心做6个圆弧运动,
其中三个
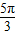 和三个
和三个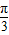 的圆弧
的圆弧故最短时间为:t=3T=
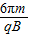
答:
(1)要使粒子能垂直DE返回到P点,从P点射出时的速度v为
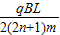 (n=0,1,2,3…).
(n=0,1,2,3…).(2)满足(1)问的粒子第一次从P点射入外部磁场到再次返回到P点仍射入外部磁场的最短时间为
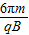 .
.点评:本题的难点在于几何图象的确定,要抓住三角形内外圆半径关系,则可得出各自圆弧所对应的圆心角,从而确定粒子运动所经历的时间.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图所示,在纸面内有两根互相平行的长直导线1和2,通有大小相等、方向相反的电流,纸面上有a、b两点,a点在两导线的中间,与两导线的距离均为r,b点在导线2右侧,与导线2的距离也为r,现测得a点的磁感应强度为B,则去掉导线1后,b点的磁感应强度大小为
如图所示,在纸面内有两根互相平行的长直导线1和2,通有大小相等、方向相反的电流,纸面上有a、b两点,a点在两导线的中间,与两导线的距离均为r,b点在导线2右侧,与导线2的距离也为r,现测得a点的磁感应强度为B,则去掉导线1后,b点的磁感应强度大小为 (2011?翠屏区模拟)如图所示,在纸面内有一匀强电场,一带正电的小球(重力不计)在一恒力F的作用下沿图中虚线由A至B做匀速运动,已知力F和AB间夹角为θ,AB间距离为d,小球带电量为q,则下列结论正确的是( )
(2011?翠屏区模拟)如图所示,在纸面内有一匀强电场,一带正电的小球(重力不计)在一恒力F的作用下沿图中虚线由A至B做匀速运动,已知力F和AB间夹角为θ,AB间距离为d,小球带电量为q,则下列结论正确的是( ) (2006?武汉模拟)如图所示,在纸面内有一匀强电场,一带负电的小球(重力不计)在一恒力F的作用下沿图中虚线由A至B做匀速运动.已知力F和AB间夹角为θ,AB间距离为d,小球带电量为q.则( )
(2006?武汉模拟)如图所示,在纸面内有一匀强电场,一带负电的小球(重力不计)在一恒力F的作用下沿图中虚线由A至B做匀速运动.已知力F和AB间夹角为θ,AB间距离为d,小球带电量为q.则( ) 如图所示,在纸面内有两根长直的平行绝缘线A和B,它们都带有均匀分布的正电荷,当它们沿各自的直线向相反方向运动时,绝缘线B所受磁力的方向是( )
如图所示,在纸面内有两根长直的平行绝缘线A和B,它们都带有均匀分布的正电荷,当它们沿各自的直线向相反方向运动时,绝缘线B所受磁力的方向是( ) (2011?湖北模拟)如图所示,在纸面内有一边长为L的等边三角形DES (虚线),三角形内只有方向垂直纸面向外的匀强磁场,三角形外部的足够大空间只有方向垂直纸面向里的匀强磁场,磁感应强度大小均为B虚线三角形DES为内外磁场的理想边界.一电量为+q、质量为m的带正电粒子从DE边中点P以速度V0垂直DE边射入三角形外部磁场,不计粒子的重力和一切阻力,试求:
(2011?湖北模拟)如图所示,在纸面内有一边长为L的等边三角形DES (虚线),三角形内只有方向垂直纸面向外的匀强磁场,三角形外部的足够大空间只有方向垂直纸面向里的匀强磁场,磁感应强度大小均为B虚线三角形DES为内外磁场的理想边界.一电量为+q、质量为m的带正电粒子从DE边中点P以速度V0垂直DE边射入三角形外部磁场,不计粒子的重力和一切阻力,试求: