题目内容
一个身高为1.50m的小孩站在竖直的平面镜前3.0m前、刚好能看见自己全身的像、他的眼晴距离地面1.40m.求镜子可能最小长度以及镜下端离地的高度.
【答案】分析:根据平面镜成像特点可知,物体与像关于平面镜对称.分别找出头顶、眼睛和脚在平面镜中的像,根据平面镜成像特点画图,结合三角形中位线可计算得平面镜长应为人身高的一半,再根据镜子的上边缘距离地面1.65m,即可求出镜子的下边缘离地面的高度.
解答:解:如图所示,A、C、B分别表示人的头顶、眼睛和脚的位置.EF为平面镜位置,由平面镜成像特点可确定A′C′B′为ACB的像,因为OC=OC′,所以OC= CC′
CC′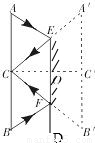
EO= A′C′,FO=
A′C′,FO= B′C′,EF=
B′C′,EF= A′B′=
A′B′= AB
AB
EF为平面镜的最小长度,AB为人的身高,这就是镜的长应为人身高的一半,即EF= ×1.5m=0.75m
×1.5m=0.75m
在三角形CBB′中FD是三角形的中位线,所以FD=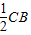 =
=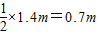
答:静止的最小长度为75cm、离地面的高度为70cm.
点评:本题考查根据平面镜成像特点的原理和解决实际问题的能力,解答此类题目的关键是画出图形,利用三角形中位线计算得平面镜的长,然后问题可解.
解答:解:如图所示,A、C、B分别表示人的头顶、眼睛和脚的位置.EF为平面镜位置,由平面镜成像特点可确定A′C′B′为ACB的像,因为OC=OC′,所以OC=
 CC′
CC′
EO=
 A′C′,FO=
A′C′,FO= B′C′,EF=
B′C′,EF= A′B′=
A′B′= AB
ABEF为平面镜的最小长度,AB为人的身高,这就是镜的长应为人身高的一半,即EF=
 ×1.5m=0.75m
×1.5m=0.75m在三角形CBB′中FD是三角形的中位线,所以FD=
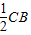 =
=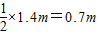
答:静止的最小长度为75cm、离地面的高度为70cm.
点评:本题考查根据平面镜成像特点的原理和解决实际问题的能力,解答此类题目的关键是画出图形,利用三角形中位线计算得平面镜的长,然后问题可解.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目