Question

质量为m=3000kg的汽车在水平公路上行驶，轮胎与路面间的最大静摩擦力为15000N，汽车经过半径为r=80m的弯路时，试问：

（1）如果汽车以速度v=36km/h沿弯路行驶，汽车的向心力为多大？是由什么力提供的？

（2）为保证汽车不发生侧滑，车速的最大值是多少？

 

Answer 1

【答案】

（1）3750 N 此向心力是由轮胎与地面的摩擦力提供的（2）40m/s

【解析】

试题分析：（1）V=36km/h=10m/s

F_向=m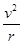=3000×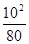N="3750" N

此向心力是由轮胎与地面的摩擦力提供的。

（2）为保证汽车不发生侧滑，则此时由最大静摩擦力提供摩擦力，

则有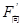=15000N，设车速的最大值为V’，

此时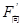=m，

得V’==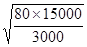m/s="40" m/s

即为保证汽车不发生侧滑，最大的车速为40m/s。

考点：牛顿第二定律；静摩擦力和最大静摩擦力；向心力．

点评：熟记摩擦力公式和向心力公式是解决本题的关键，分析向心力是由哪些力提供的．通常这样找向心力：沿半径方向的所有力的合力提供该物体做圆周运动的向心力．