��Ŀ����
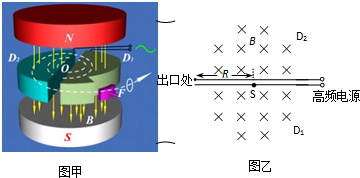
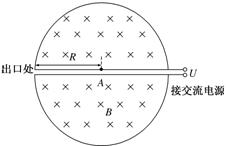
1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м���������Ϊd�����Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ��A������Դ���������ӣ�����Ϊm�������Ϊ+q ���ڼ������б����٣����ٵ�ѹΪU�����ٹ����в����������ЧӦ���������á�
��1�������ӵ�2�κ͵�1�ξ�����D�κм���������뾶֮�ȣ�
��2�������ӴӾ�ֹ��ʼ���ٵ����ڴ�(�糡�ʹų�)�������ʱ��t��
![]()
![]() +
+![]()
����:
��1�����ӵ�һ�ν���糡����
eu=1/2*m(v1)2
�����ڴų���
qvB=m(v1)2/r1
���ӵڶ��ν���糡����
2eu=1/2*m(v2)2
�����ڴų���
qvB=m(v2)2/r2
����ʽ��r1��r2=��2��1
��2���ڵ糡��
v2t1/2=d
�ڴų���
t2=��r1/v1+��r2/v2
T=t1+t2
����T+

��ϰ��ϵ�д�
�����Ŀ

 ��2009?���գ�1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ��A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ������б����٣����ٵ�ѹΪU�����ٹ����в����������ЧӦ���������ã�
��2009?���գ�1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ��A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ������б����٣����ٵ�ѹΪU�����ٹ����в����������ЧӦ���������ã�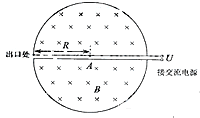 1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ��A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ������б����٣����ٵ�ѹΪU�����ٹ����в������������ã�
1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ��A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ������б����٣����ٵ�ѹΪU�����ٹ����в������������ã�