Question

(18分) 如图所示，轻质长绳水平地跨过相距的两个定滑轮A、B上，质量为的物块悬挂在绳上O点，O与A、B两滑轮的距离相等，在轻绳两端C、D分别施加竖直向下的恒力，先托住物块，使绳处于水平拉直状态. 从静止释放物块，在物块下落过程中，保持C、D两端的拉力不变，则：

（1）当物块下落距离为多大时，物块的加速度为零.
（2）当物块下落上述距离的过程中，克服C端恒力做的功为多少?
（3）求物体下落的最大速度和最大距离.

Answer 1

(1) (2)  (3) ,

解析试题分析：：（1）当物块所受的合外力为零时，加速度为零，此时物块下降距离为．
因恒定，所以两绳对物块拉力大小分别为，两绳与竖直方向夹角均为，由平衡条件知：
,所以
由图知： ①
（2）物块下落时，绳的C、D端均上升,由几何关系可得： ②
克服C端恒力F的功为： ③
由①②③式联立解得：
（3）在物块下落过程中，共有三个力对物块做功．重力做正功，两端绳子对物块的拉力做负功．两端绳子拉力做的功就等于作用在C、D端的恒力F所做的功．
因物块下降距离时动能最大．由动能定理得： ④
将①②③式代入④式解得：
当物块速度减小为零时，物块下落距离达到最大值，绳C、D上升的距离为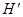．由动能定理得：
，又
联立解得：
考点：本题考查了动能定理的应用、力的合成与分解的运用、共点力平衡的条件及其应用.