题目内容
如图所示，AB为光滑竖直杆，ACB为构成直角的光滑L形直轨道，C处有一小圆弧连接可使小球顺利转弯（即通过转弯处不损失机械能）。套在AB杆上的小球自A点静止释放，分别沿AB轨道和ACB轨道运动，如果沿ACB轨道运动的时间是沿AB轨道运动时间的1.5倍，则BA与CA的夹角为
| A．30º | B．45º | C．53º | D．60º |
C
解析试题分析：设BA 与CA的夹角为α，AB的长度为L，小球沿AB下滑做自由落体运动，由
得
；沿ACB运动时分两个阶段AC和CB，分别作初速度为零的匀加速运动和初速度不为零的匀加速运动，由A到C，
，解得
，从C到B，
，所以有
，又因为
，代入解得
，即
，故选项C正确．
考点：匀变速运动规律．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
ａ、ｂ两物体同时、同地、同向做匀变速直线运动，若加速度相同，初速度
不同，则在运动过程中，下列说法正确的是
| A．ａ、ｂ两物体速度之差保持不变 |
| B．ａ、ｂ两物体速度之差与时间成正比 |
| C．ａ、ｂ两物体位移之差与时间成正比 |
| D．ａ、ｂ两物体位移之差与时间平方成正比 |
如图所示为一物体做直线运动的速度v-t图象，根据图象做出的以下判断中，正确的是
| A．物体始终沿正方向运动 |
| B．物体先沿负方向运动，在t=2s后开始沿正方向运动 |
| C．在t=2s前后物体的加速度方向相反 |
| D．在t=2s时，物体回到了原点，即出发点 |
如图所示，圆柱形的仓库内有三块长度不同的滑板aO、bO、cO，其下端都固定于底部圆心O，而上端则搁在仓库侧壁上，三块滑板与水平面的夹角依次是30°、45°、60°.若有三个小孩同时从a、b、c处开始下滑(忽略阻力)，则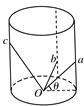
| A．a处小孩最先到O点 | B．b处小孩最先到O点 |
| C．c处小孩最先到O点 | D．三个小孩同时到O点 |
一辆摩托车与一辆汽车在平直的公路上运动，下表是每隔1秒记录的两车的速度值。若两车的运动可看做匀变速直线运动，则下列说法正确的是
 | 0 | 1 | 2 | 3 | 4 | |
| 摩托车 |  | 18.0 | 17.5 | 17.0 | 16.5 | 16.0 |
| 汽车 |  | 9.8 | 11.0 | 12.2 | 13.4 | 14.6 |
B. 在0～4s内，汽车的平均速度较大
C. 摩托车的位移在减小
D. 从t＝4s开始计时，经过
两车的速度相等 物体做匀加速直线运动时，下列说法中正确的是：( )
| A．速度总是与时间成正比． |
| B．速度的增加量与时间的比值均匀增大． |
| C．任意两个连续相等的时间间隔里的位移之差一定相等． |
| D．在任意时间段内的平均速度一定是（v0+ vt）/2． |
一辆公共汽车进站后开始刹车，做匀减速直线运动．开始刹车后的第1 s内和第2 s内位移大小依次为9 m和7 m．则刹车后6 s内的位移是( )
| A．20 m | B．24 m | C．25 m | D．75 m |