题目内容
如图所示，斜面的倾角为α，质量为m的小球以v0的速度水平抛出，落在斜面上的P点（P点图中未画出）．求：（1）小球经多长时间离斜面最远？
（2）小球离斜面的最远距离是多少？（重力加速度为g）
分析：平抛运动是具有水平方向的初速度只在重力作用下的运动，是一个匀变速曲线运动．解决平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动．
解答：解：（1）当速度与斜面平行时，与斜面距离最远，
此时tanα=
得：vy=v0tanα
所以：t=
=
；
（2）由平抛运动的规律可知：A点为水平位移的中点，所以有：OA=
x=
v0t
即：AB=OAsinα
得：AB=
．
答：（1）小球经
离斜面最远；
（2）小球离斜面的最远距离是
此时tanα=| vy |
| v0 |
得：vy=v0tanα
所以：t=
| vy |
| g |
| v0tanα |
| g |
（2）由平抛运动的规律可知：A点为水平位移的中点，所以有：OA=
| 1 |
| 2 |
| 1 |
| 2 |
即：AB=OAsinα
得：AB=
| v02tanαsinα |
| 2g |
答：（1）小球经
| v0tanα |
| g |
（2）小球离斜面的最远距离是
| v02tanαsinα |
| 2g |
点评：本题是对平抛运动基本概念和基本公式的考察，难度不大，本题是将位移分解成水平和竖直两个方向，由位移公式求解．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，斜面的倾角θ=37°．一个质量m=1.0kg的物体，从静止开始沿斜面下滑．在开始运动后的最初2.0s内，物体下滑的距离为4.0m．不计空气阻力．计算时重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．
如图所示，斜面的倾角为θ，圆柱体质量为m．若把重力沿垂直于墙面和垂直于斜面两个方向分解，则重力垂直于斜面的分力大小为
如图所示，斜面的倾角为α，人用跨过定滑轮的绳子拉小车．现人以速度v匀速拉动绳子，当拉小车的绳子与斜面的夹角为β时，小车沿斜面运动的速度为（ ）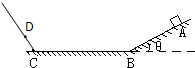
如图所示，斜面的倾角θ=37°，一物块从斜面A点由静止释放．物块质量m=10kg，物块与水平面的动摩擦因数μ=0.4，其余部分光滑，不计物块滑至B、C点时由于碰撞的能量损失，最后能够上升到D点．已知AB高度差H=1.8m，CD高度差为h=0.6m，（取g=10m/s2，sin37°=0.6，cos37°=0.8）（ ）