题目内容
将一根粗细均匀、质量为M的铁丝弯成直角,两直角边边长之比AC:BC=m:n(m>n),C点可绕竖直面转动,如图所示,当直角铁丝静止时,BC边与竖直方向的夹角为θ,则sinθ= ,若在B点悬挂一物体,将使θ=45°,则该物体的质量为 .
【答案】分析:(1)铁丝均匀,两边铁丝的重心分别在其中点,两边质量之比等于长度之比,可求两边重力之比;求出两边力臂之比,根据力矩平衡条件列式求sinθ的大小;
(2)在B点悬挂一物体,根据力矩平衡条件和两边铁丝的质量关系,求得在B点所挂物体c的质量.
解答: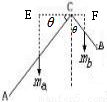 解:(1)如图,两边的重心分别在中点,质量之比等于长度之比,则
解:(1)如图,两边的重心分别在中点,质量之比等于长度之比,则
重力之比:Ga:Gb=mag:mbg=ma:mb=m:n,
左边力臂:
La= AC×cosθ,
AC×cosθ,
右边力臂:
Lb= BC×sinθ,
BC×sinθ,
由杠杆平衡条件可知:
Ga×La=Gb×Lb,
即:Ga× AC×cosθ=Gb×
AC×cosθ=Gb× BC×sinθ,
BC×sinθ,
∴sinθ= ×cosθ=
×cosθ=

解得:
sinθ= ;
;
(2)在B点悬挂一物体,θ=45°,如右图,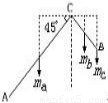
Ga× AC×cos45°=Gb×
AC×cos45°=Gb× BC×sin45°+GC×BC×sin45°…①
BC×sin45°+GC×BC×sin45°…①
∵ma:mb=m:n,总质量为M,
∴ma=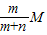 ,mb=
,mb=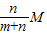 ,
,
又AC:BC=m:n,Ga:Gb=m:n,都代入①式得:mc=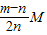
故答案为: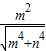 ;
;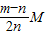 .
.
点评:本题考查了学生对力矩平衡条件的掌握和运用,能画出杠杆示意图、利用好数学知识是本题的关键.
(2)在B点悬挂一物体,根据力矩平衡条件和两边铁丝的质量关系,求得在B点所挂物体c的质量.
解答:
 解:(1)如图,两边的重心分别在中点,质量之比等于长度之比,则
解:(1)如图,两边的重心分别在中点,质量之比等于长度之比,则重力之比:Ga:Gb=mag:mbg=ma:mb=m:n,
左边力臂:
La=
 AC×cosθ,
AC×cosθ,右边力臂:
Lb=
 BC×sinθ,
BC×sinθ,由杠杆平衡条件可知:
Ga×La=Gb×Lb,
即:Ga×
 AC×cosθ=Gb×
AC×cosθ=Gb× BC×sinθ,
BC×sinθ,∴sinθ=
 ×cosθ=
×cosθ=

解得:
sinθ=
 ;
;(2)在B点悬挂一物体,θ=45°,如右图,

Ga×
 AC×cos45°=Gb×
AC×cos45°=Gb× BC×sin45°+GC×BC×sin45°…①
BC×sin45°+GC×BC×sin45°…①∵ma:mb=m:n,总质量为M,
∴ma=
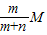 ,mb=
,mb=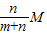 ,
,又AC:BC=m:n,Ga:Gb=m:n,都代入①式得:mc=
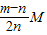
故答案为:
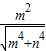 ;
;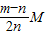 .
.点评:本题考查了学生对力矩平衡条件的掌握和运用,能画出杠杆示意图、利用好数学知识是本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目


 将一根粗细均匀、质量为M的铁丝弯成直角,两直角边边长之比AC:BC=m:n(m>n),C点可绕竖直面转动,如图所示,当直角铁丝静止时,BC边与竖直方向的夹角为θ,则sinθ=
将一根粗细均匀、质量为M的铁丝弯成直角,两直角边边长之比AC:BC=m:n(m>n),C点可绕竖直面转动,如图所示,当直角铁丝静止时,BC边与竖直方向的夹角为θ,则sinθ= 一根粗细均匀全长为40厘米、一端封闭的直玻璃管,用长为19厘米的汞柱封闭一定质量的空气.开始时,玻璃管开口向下竖直放置,管内空气柱长为18.2厘米,温度为0℃.大气压强为76cmHg,1cmHg=1333Pa.
一根粗细均匀全长为40厘米、一端封闭的直玻璃管,用长为19厘米的汞柱封闭一定质量的空气.开始时,玻璃管开口向下竖直放置,管内空气柱长为18.2厘米,温度为0℃.大气压强为76cmHg,1cmHg=1333Pa.