题目内容
质量相同的两小球,分别用长L和2L的细绳挂在天花板上,分别拉起小球使绳伸直呈水平状态,然后轻轻释放.当小球到达最低位置时( )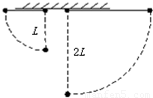
A.两球运动的线速度相等
B.两球运动的角速度相等
C.两球的向心加速度相等
D.细绳对两球的拉力相等
【答案】分析:根据动能定理或机械能守恒定律判断出最低点的速度跟什么因素有关,再根据向心加速度a=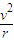 ,比较出向心加速度的大小,通过受力分析,合力提供向心力,比较出拉力的大小.
,比较出向心加速度的大小,通过受力分析,合力提供向心力,比较出拉力的大小.
解答:解:A、根据动能定理mgl=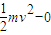 ,
,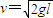 ,知右边小球线速度大.故A错误.
,知右边小球线速度大.故A错误.
B、根据ω=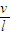 =
=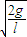 ,知两球的角速度不等.故B错误.
,知两球的角速度不等.故B错误.
C、向心加速度a=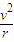 =2g,与l无关.所以两球的向心加速度相等.故C正确.
=2g,与l无关.所以两球的向心加速度相等.故C正确.
D、根据F-mg=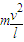 ,F=3mg,所以细绳对两球拉力大小相等.故D正确.
,F=3mg,所以细绳对两球拉力大小相等.故D正确.
故选CD.
点评:解决本题的关键是根据动能定理求出小球最低点的速度,再根据a=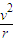 ,ω=
,ω=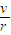 分析向心加速度和角速度.
分析向心加速度和角速度.
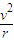 ,比较出向心加速度的大小,通过受力分析,合力提供向心力,比较出拉力的大小.
,比较出向心加速度的大小,通过受力分析,合力提供向心力,比较出拉力的大小.解答:解:A、根据动能定理mgl=
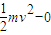 ,
,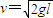 ,知右边小球线速度大.故A错误.
,知右边小球线速度大.故A错误.B、根据ω=
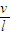 =
=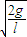 ,知两球的角速度不等.故B错误.
,知两球的角速度不等.故B错误.C、向心加速度a=
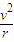 =2g,与l无关.所以两球的向心加速度相等.故C正确.
=2g,与l无关.所以两球的向心加速度相等.故C正确.D、根据F-mg=
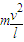 ,F=3mg,所以细绳对两球拉力大小相等.故D正确.
,F=3mg,所以细绳对两球拉力大小相等.故D正确.故选CD.
点评:解决本题的关键是根据动能定理求出小球最低点的速度,再根据a=
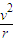 ,ω=
,ω=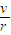 分析向心加速度和角速度.
分析向心加速度和角速度. 
练习册系列答案
相关题目
 (1)用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若测得各落点痕迹到O点的距离:OM=2.68cm,OP=8.62cm,ON=11.50cm,并知A、B两球的质量比为2:1,则未放B球时A球落地点是记录纸上的
(1)用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若测得各落点痕迹到O点的距离:OM=2.68cm,OP=8.62cm,ON=11.50cm,并知A、B两球的质量比为2:1,则未放B球时A球落地点是记录纸上的









 = %(结果保留一位有效数字).
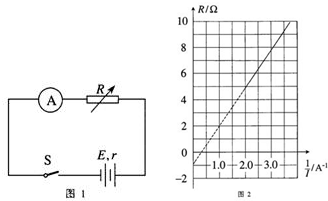
= %(结果保留一位有效数字). 图线,其中R为电阻箱读数,I为电流表读数,由此可以得到E= V,r= Ω.
图线,其中R为电阻箱读数,I为电流表读数,由此可以得到E= V,r= Ω.

